Séance 2
Contents
Séance 2¶
Objectifs de la séance¶
Etude de système d’ordre 2
Analyse de la réponse indicielle
Influence de zeta sur les caractéristiques temporelles : dépassement, temps de réponse, …
Lien entre ces caractéristiques et la position des pôles
Réponse indicielle du \(2^{nd}\) ordre générale paramétrée¶
Soit un système du second ordre : \( G(p)=\frac{K}{(\frac{p}{\omega_n})^2+\frac{2\zeta}{\omega_n}p+1} \) (cf. page 3-6)
Analysez les réponses typiques pour les valeurs caractéristiques de zeta :[0.1, 0.2, 0.3, 0.42, 0.5, 0.6, 0.7, 0.8, 1, 1.41, 2, 6, 10] (cf. page 3-9). Créez un script qui permette de tracer de manière itérative les différentes fonctions dont les différents zeta seront encodés dans une liste.
K=1
wn=1
# Définition des coefficients d'amortissement
zeta_values =[0.1, 0.2, 0.3, 0.4, 0.42, 0.5, 0.6, 0.7, 0.8, 1, 1.41, 2, 6, 10]
# Création de la fenêtre à une taille donnée
fig = plt.figure("Steps",figsize=(20,10))
# Réponse indicielle
# Calcule les différentes fonctions de transfert ainsi que la réponse indicielle
for zeta in zeta_values:
G = ml.tf(K, [(1/wn)**2, 2*zeta/wn, 1]) # Calcul de la fonction de transfert
rlf.step_(G, NameOfFigure='Steps', sysName=zeta); # Traçage de la réponse indicielle
Note
La ligne de code
fig = plt.figure("Steps",figsize=(20,10))
n’a aucune utilité pour vous dans Spyder, elle permet juste d’ouvrir une fenêtre d’une largeur de 20” et de 10” de haut afin d’éviter d’avoir des graphes qui ne soient trop petits pour être lisibles sur cette page.
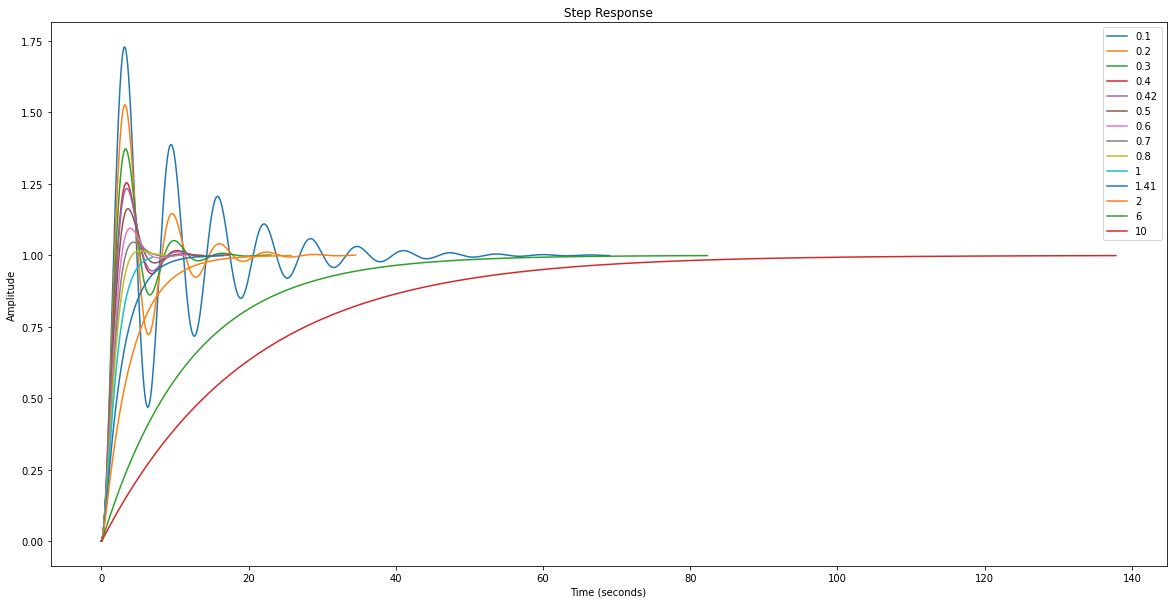
Commentaires sur les courbes¶
……………………………………………..
……………………………………………..
Si \(\zeta < 1\) : Il y a un dépassement et celui-ci est d’autant plus grand que \(\zeta\) est faible.
Si \(\zeta \geqslant 1\) : Il n’y a pas de dépassement (système suramorti).
(cf. page 3-9)
Dépassement¶
Visualisez la valeur du dépassement pour les différentes valeurs de zeta et regardez l’influence de zeta sur la valeur du dépassement sur l’abaque de la page 3-11 : D ……. si zeta ……
D \(\searrow\) si \(\zeta \nearrow\)
Observez que les échelles de cet abaque sont logarithmiques. Par exemple, observez la valeur du dépassement lorsque zeta=0.5, sur la figure et indiquez clairement la position de ce point sur l’abaque.
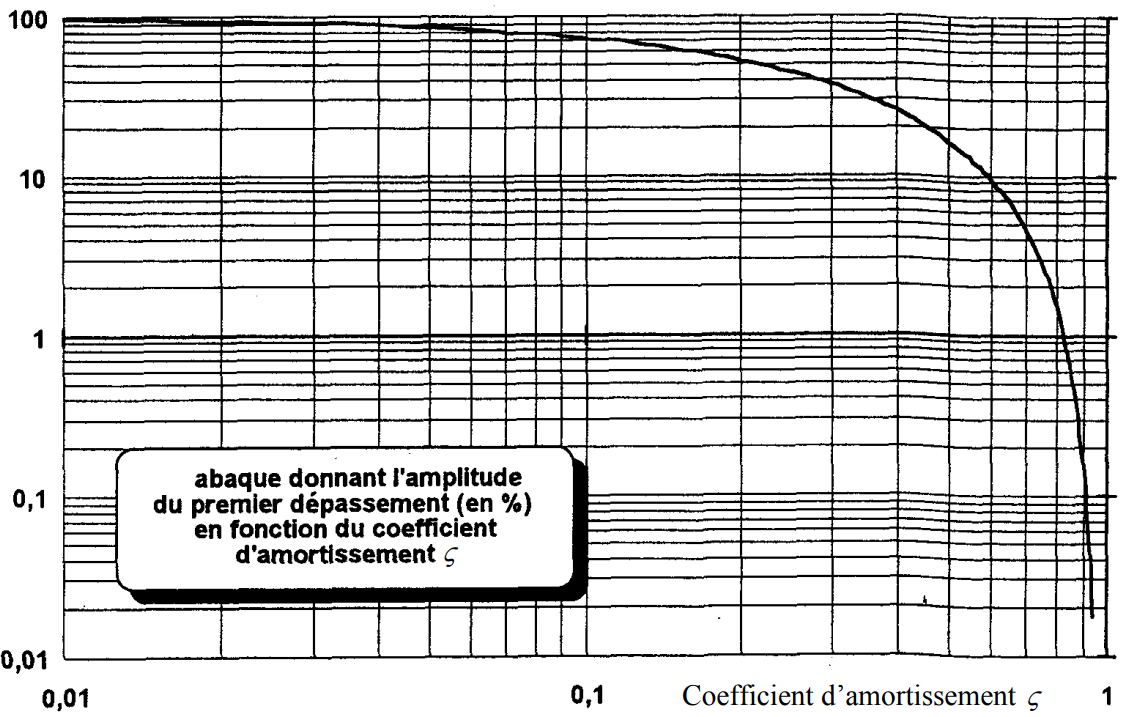
Vérifiez par calcul :
\( D_p=100*e^{-\frac{k\pi\zeta}{\sqrt{1-\zeta^2}}} \)
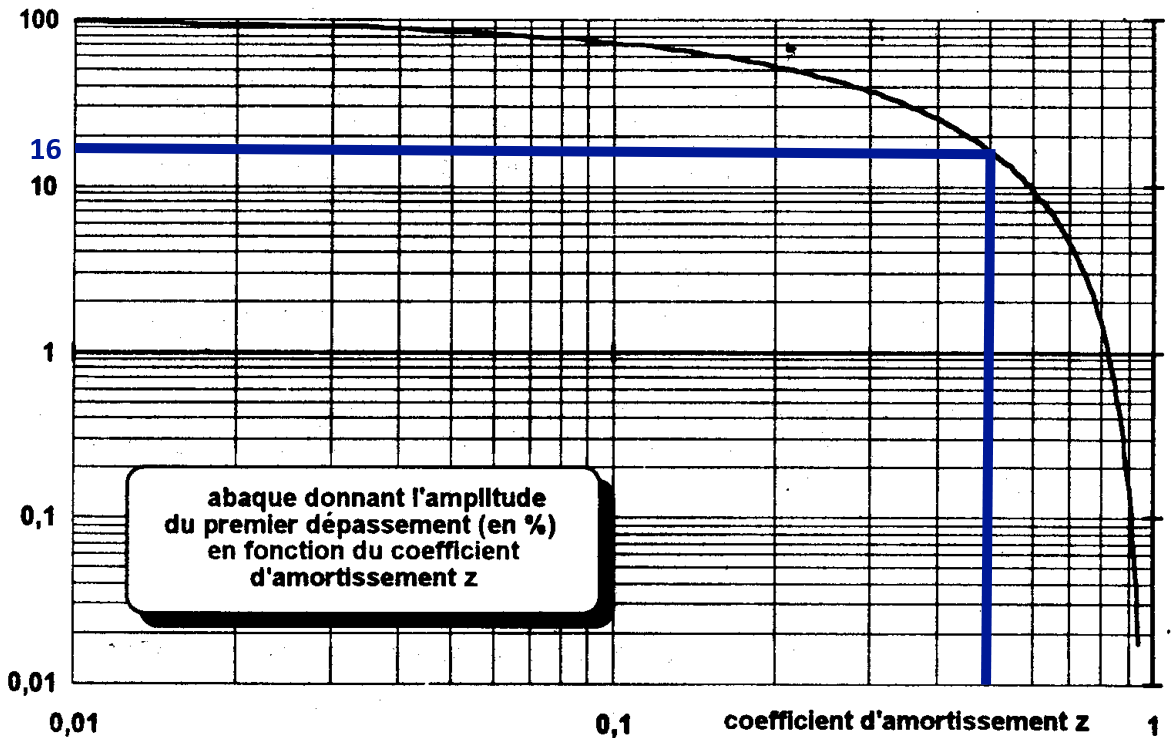
Par calcul: \(D_p=16.3\%\)
Pseudo pulsation¶
Observez l’influence du coefficient d’amortissement sur la pulsation d’oscillation \(\omega_d\) : \(\omega_d\) … si \(\zeta\) …
\(\omega_d \nearrow\) si \(\zeta \searrow\)
Si \(\zeta < 1\) : Il y a des oscillations et celles-ci sont d’autant plus grandes que \(\zeta\) est faible.
Si \(\zeta \geqslant 1\) : Il n’y a pas d’oscillations.
(cf. page 3-6 à 3-7)
Temps de réponse à 5%¶
Visualisez la valeur du temps de réponse à 5 % pour les différentes valeurs de \(\zeta\) et regardez l’influence de \(\zeta\) sur l’abaque de la page 3-12.
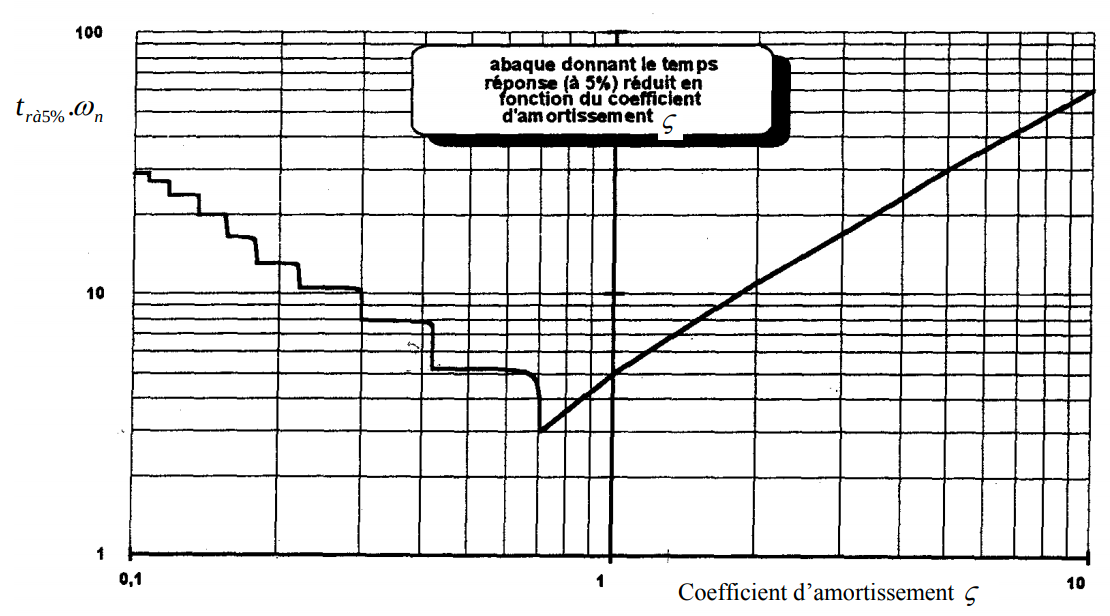
Expliquez l’allure particulière de cette courbe :
si \(\zeta\) > 0.7: …
en \(\zeta\) = 0.7: …
si \(\zeta\) < 0.7: « escaliers » dans la partie gauche car …
si \(\zeta\) > 0.7: comportement d’un système d’ordre 1.
en \(\zeta\) = 0.7: le système possède le \(t_{r_{5\%}}\) le plus faible possible => système le plus rapide à se stabiliser possible.
si \(\zeta\) < 0.7: « escaliers » dans la partie gauche car il y a des oscillations qui font sortir le système de la plage des 5% de tolérance autour de la valeur atteinte en régime établi.
Note
Le nombre de “marches” équivaut au nombre de dépassements des valeurs limites 0.95 et 1.05.
Pourquoi le \(t_{r_{5\%}}\) est-il “identique” pour un \(\zeta\) de 0,6 ou 0,5 ?
Le \(t_{r_{5\%}}\) est “identique” pour un \(\zeta\) de 0,6 ou 0,5 car ils se trouvent sur la même “marche”.
Vérifiez via Python
K=1
wn=1
# Définition des coefficients d'amortissement
zeta_values =[0.1, 0.2, 0.3, 0.4, 0.42, 0.5, 0.6, 0.7, 0.8, 1, 1.41, 2, 6, 10]
# Création de la fenêtre à une taille donnée
fig = plt.figure("Steps",figsize=(20,10))
ax = fig.subplots()
# Réponse indicielle
# Calcule les différentes fonctions de transfert ainsi que la réponse indicielle
for zeta in zeta_values:
G = ml.tf(K, [(1/wn)**2, 2*zeta/wn, 1]) # Calcul de la fonction de transfert
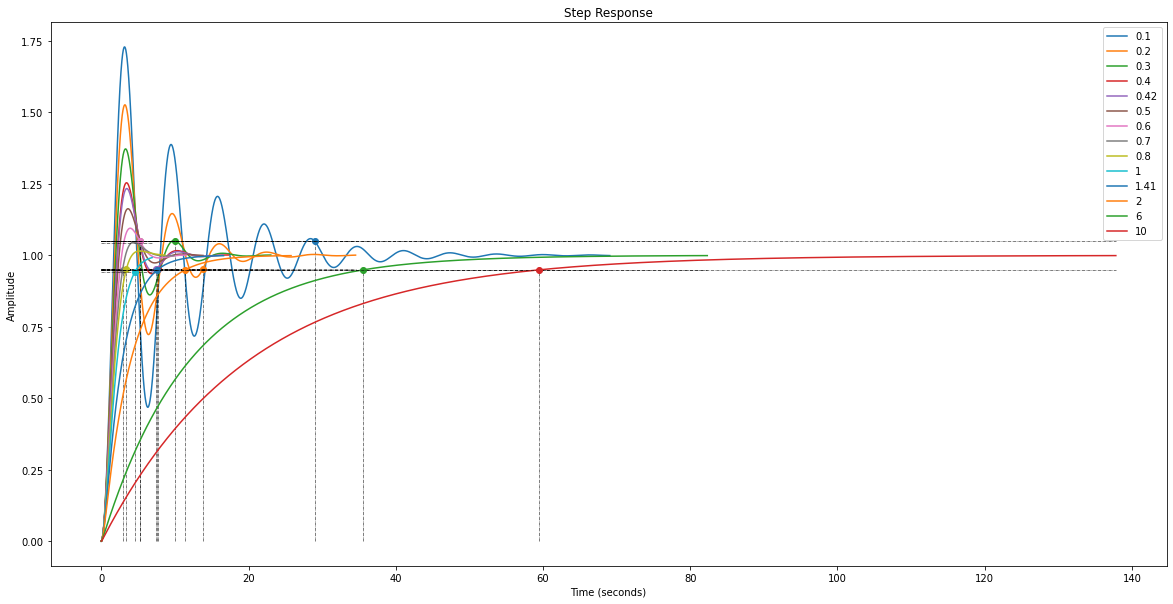
rlf.stepWithInfo(G, NameOfFigure='Steps', sysName=zeta, plot_rt=False, plot_overshoot=False, plot_DCGain=False); # Traçage de la réponse indicielle avec juste le point du tr5%
Position des pôles¶
Vous pouvez faire le lien entre l’allure de la réponse indicielle et la position des pôles dans le plan complexe tracé par la fonction pzmap(h).
# Création de la fenêtre à une taille donnée
fig = plt.figure("Pole Zero Map",figsize=(20,10))
ax = fig.subplots()
# Pour pouvoir boucler sur lnombrees couleurs standards afin de directement jouer avec les couleurs des graphes
from itertools import cycle
prop_cycle = plt.rcParams['axes.prop_cycle']
colors = cycle(prop_cycle.by_key()['color'])
# Trace les poles et zéros pour chacune des fonctions de transfert stockées dans 'g'
for zeta in zeta_values:
G = ml.tf(K, [(1/wn)**2, 2*zeta/wn, 1]) # Calcul de la fonction de transfert
poles, zeros = rlf.pzmap(G, NameOfFigure="Pole Zero Map", sysName=zeta, color=next(colors));
plt.plot([poles.real[0], 0], [0, 0], 'k:'); # Ligne horizontale passant par 0 pour marquer l'axe des imaginaires

Pour chaque valeur de \(\zeta\), la fonction pzmap vous trace 2 croix pour indiquer les 2 pôles du système dans le plan complexe :
Pour \(\zeta=10\), les pôles sont en : ……… et ………
C’est le pôle en ……… qui domine dans le tracé de la réponse indicielle car ………
Si \(\zeta\) \(\searrow\) jusque \(\zeta=1\), les pôles se déplacent ………
Si \(\zeta<1\), les pôles deviennent ………
Si \(\zeta\) \(\searrow\) encore, les pôles se déplacent ………
Pour \(\zeta=10\), les pôles sont en : -19.9 et -0.05
C’est le pôle en -0.05 qui domine dans le tracé de la réponse indicielle car \(\tau=\frac{-1}{p}\). La constante de temps est donc plus grande.
Si \(\zeta\) \(\searrow\) jusque \(\zeta=1\), les pôles se déplacent sur l’axe des réels (vers la gauche pour les pôles dominants, vers la droite pour les autres).
Si \(\zeta<1\), les pôles deviennent complexes conjugués.
Si \(\zeta\) \(\searrow\) encore, les pôles se déplacent sur l’axe des imaginaires et l’axe des réels. La valeur absolue de la partie imaginaire (oscillations) \(\nearrow\), et la valeur absolue de la partie réelle (amortissement) \(\searrow\).
Observez l’influence des pôles réels par rapport aux pôles complexes : …
Si les pôles du système sont réels alors le système se comporte comme un système du \(1^{er}\) ordre \(\Rightarrow\) Pas d’oscillations.
Si par contre, ses pôles sont complexes, le système oscille.
et si \(\zeta<0\) : …
Si \(\zeta<0\), le système est instable!
Exercice 1¶
Soit un système asservi à retour unitaire décrit par la fonction de transfert :
Etude de la réponse indicielle¶
num = 8
den = [1, 1, 10]
H_BF = ml.tf(num, den)
rlf.step_(H_BF);
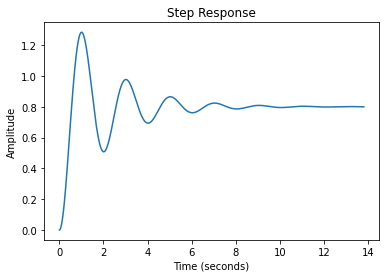
La fonction présente 2 pôles complexes conjugués et les constantes associées à sa réponse sont:
w, zetas, poles = ml.damp(H_BF);
_____Eigenvalue______ Damping___ Frequency_
-0.5 +3.122j 0.1581 3.162
-0.5 -3.122j 0.1581 3.162
Vous pouvez le vérifier en identifiant à la représentation canonique (p. 3-6) : …
1°) Mise sour forme canonique:
2°) Identification:
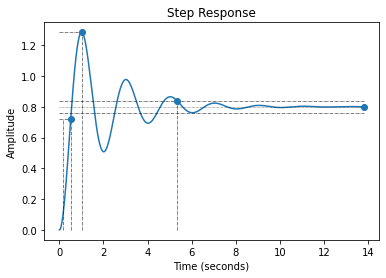
Déterminez les caractéristiques de la réponse par les abaques :
le dépassement (\(D_\%\)) = ……………
le temps de réponse à 5% (\(t_{r_{5\%}}\)) = ……………
le dépassement (\(D_\%\)) \(\approx\) 60%
le temps de réponse à 5% (\(t_{r_{5\%}}\)) \(\approx \frac{16}{3.16} = 5\) s
et comparez avec les caractéristiques fournies par stepWithInfo :
la valeur atteinte en régime établi (DCGain) = ……………
l’erreur statique (\(\varepsilon_0\)) = ……………
le temps de réponse à 5% (\(t_{r_{5\%}}\)) = ……………
le temps de montée (\(t_m\)) = ……………
le dépassement (\(D_\%\)) = ……………
l’instant du premier pic (\(t_{peak}\)) = ……………
info = rlf.stepWithInfo(H_BF)
rlf.printInfo(info)
print("Erreur statique :", (1-info.DCGain)*100, "%")
DCGain : 0.7995637249145586
Overshoot : 60.55544633040029
Peak : 1.2837431072325436
PeakTime : 1.005869755595359
RiseTime : 0.36752933377522723
SettlingTime : 5.334702096639671
Erreur statique : 20.043627508544137 %
Exercice 2¶
L’application 2 d’asservissement de position est décrite par le schéma bloc :
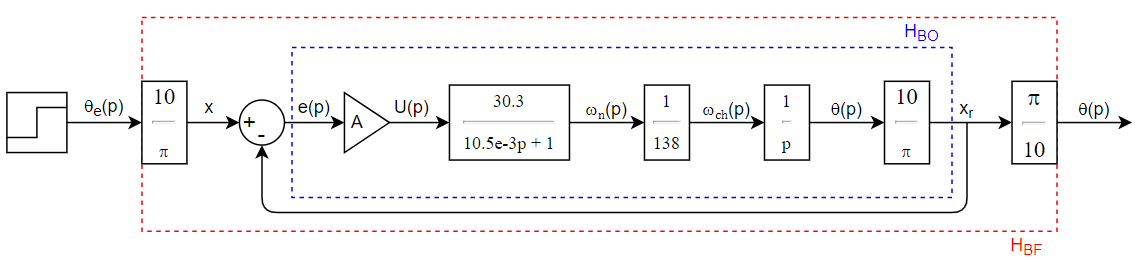
où A représente un correcteur proportionnel.
La fonction de transfert en BF de l’application d’asservissement de vitesse est :
Utilisez les abaques ou équations pour :
Prédire l’allure de la réponse indicielle du système si A=99 :
dépassement : ……………
temps de réponse : ……………
\[\begin{split} \begin{alignat*}{2} \left\{ \begin{aligned} \begin{array}{ll} \frac{2\zeta}{\omega_n} = \frac{10.875*10^{-3}}{A+1} \\ \frac{1}{\omega_n^2} = \frac{1.36*10^{-6}}{A+1} \end{array} \end{aligned}\right. \Rightarrow \left\{ \begin{aligned} \begin{array}{ll} \zeta = \frac{10.875*10^{-3}}{100}*\frac{8574.93}{2} = 0.466 \\ \omega_n = \sqrt{\frac{100}{1.36*10^{-6}}} = 8574.93 rad/s \end{array} \end{aligned}\right. \end{alignat*}\ \end{split}\]dépassement : \( D_p=100*e^{-\frac{\pi*0.466}{\sqrt{1-0.466^2}}} = 19.09\% \)
temps de réponse à 5%: \( \frac{5.3}{8574.93} = 618 µs \)
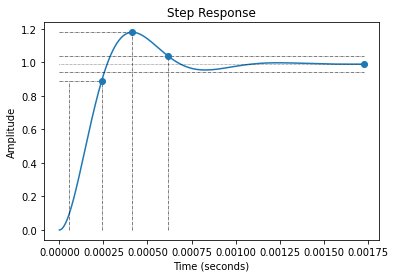
Vérifiez en traçant les réponses via python.
A = 99
num = A/(A+1)
den = [1.36e-6/(A+1), 10.875e-3/(A+1), 1]
H_BF = ml.tf(num, den)
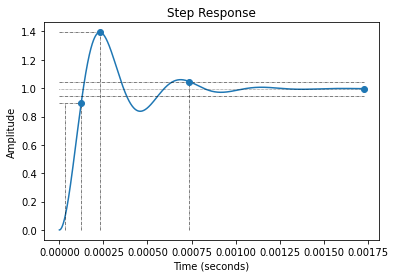
info = rlf.stepWithInfo(H_BF)
print("Dépassement :", info.Overshoot, "%")
print("Temps de réponse à 5% :", info.SettlingTime, "s")
Dépassement : 19.228357919246108 %
Temps de réponse à 5% : 0.0006151343954389906 s
Déterminer le correcteur A si on veut un dépassement de 40% :
\[ D_p=100*e^{-\frac{k\pi\zeta}{\sqrt{1-\zeta^2}}} \Rightarrow 40 = 100*e^{-\frac{k\pi\zeta}{\sqrt{1-\zeta^2}}} \Rightarrow \zeta=0.28 \]\[\begin{split} \begin{alignat*}{2} \left\{ \begin{aligned} \begin{array}{ll} \frac{2*0.28}{\omega_n} = \frac{10.875*10^{-3}}{A+1} \\ \frac{1}{\omega_n^2} = \frac{1.36*10^{-6}}{A+1} \end{array} \end{aligned}\right. \Rightarrow \left\{ \begin{aligned} \begin{array}{ll} A = 276 \\ \omega_n = 14279 rad/s \end{array} \end{aligned}\right. \end{alignat*}\ \end{split}\]Vérifiez en traçant les réponses via python.
A = 276
num = A/(A+1)
den = [1.36e-6/(A+1), 10.875e-3/(A+1), 1]
H_BF = ml.tf(num, den)
info = rlf.stepWithInfo(H_BF)
print("Dépassement :", info.Overshoot, "%")
Dépassement : 39.95296631023082 %