Séance 4
Contents
Séance 4¶
Objectifs de la séance¶
Analyse de la réponse à un saut de consigne
Extrapolation à partir de la réponse indicielle
Tracé du signal
Tracé des différents diagrammes fréquentiels
Effet d’un correcteur proportionnel dans les différents diagrammes fréquentiels
Réponse à une variation quelconque de consigne¶
Pour un système asservi à retour unitaire dont la fonction de transfert de boucle ouverte s’écrit :
Nous voudrions connaître l’évolution de la sortie si la consigne passe de 10° à 30° :
A partir de la réponse indicielle normée¶
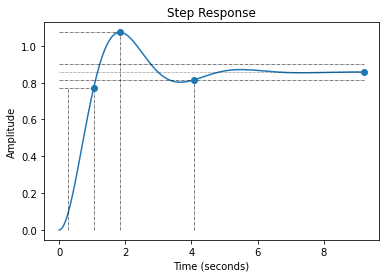
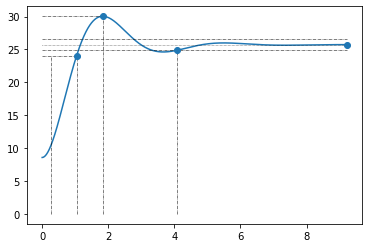
Tracez tout d’abord la réponse indicielle et relevez-en les grandeurs caractéristiques:
Régime établi = …
Dépassement relatif = …
\(t_{r_{5\%}}\) = …
G_BO = ml.tf(6, [2, 3, 1])
G_BF = ml.feedback(G_BO, 1)
info = rlf.stepWithInfo(G_BF, NameOfFigure='Step with infos')
print("- Régime établi =", info.DCGain,
"\n- Dépassement relatif =", info.Overshoot, "%",
"\n- tr_5% =", info.SettlingTime, "s\n")
- Régime établi = 0.8580265483248184
- Dépassement relatif = 25.161365744447806 %
- tr_5% = 4.077825465220377 s
En déduire l’allure du signal de sortie si le signal d’entrée est celui donné à la figure suivante :
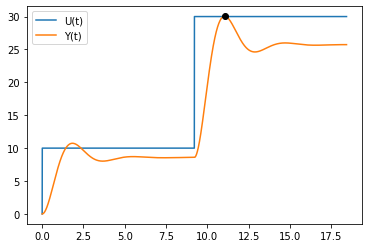
Calculs:
de la valeur initiale:
de la valeur finale:
du dépassement absolu:
du dépassement relatif:
Valeur initiale = \(10*\frac{6}{7} = 8.571\)
Valeur finale = \(30*\frac{6}{7} = 25.714\)
Dépassement absolu = \(8.571+(25.714-8.571)*(1+0.252) = 30.028\)
Dépassement relatif = \((\frac{30.028}{25.714}-1)*100 = 16.774\%\)
Note
Dépassement relatif de référence = 25.2% (cf. valeur calculée précédemment)
Via Python¶
import warnings # Package permettant de gérer l'affichage de messages d'erreurs
warnings.filterwarnings('ignore') # Pour éviter d'afficher un message d'erreur inutile
peak, peakTime, __, __ = rlf.stepFromTo(G_BF, 10, 30, focus=False)
warnings.resetwarnings() # Pour réactiver l'affichage d'erreurs
print("D_abs =", peak)
print("T_dep =", peakTime, "s\n")
D_abs = 30.04754144710496
T_dep = 1.8328577340232597 s
Astuce
La fonction stepFromTo peut également limiter l’affichage à juste la partie intéressante du step et ainsi permettre d’utiliser la fonction stepInfo pour afficher toutes les infos que l’on souhaite obtenir.
warnings.filterwarnings('ignore') # Pour éviter d'afficher un message d'erreur inutile
peak, peakTime, yout, t = rlf.stepFromTo(G_BF, 10, 30, focus=True)
warnings.resetwarnings() # Pour réactiver l'affichage d'erreurs
info = rlf.step_info(yout, t)
rlf.printInfo(info)
print("") # Pour laisser une ligne vide après l'affichage des infos afin de les séparer de ce qui suit
DCGain : 25.73194794895096
Overshoot : 16.771343960105977
Peak : 30.04754144710496
PeakTime : 1.8328577340232597
RiseTime : 0.7847209996923704
SettlingTime : 4.076496648636657
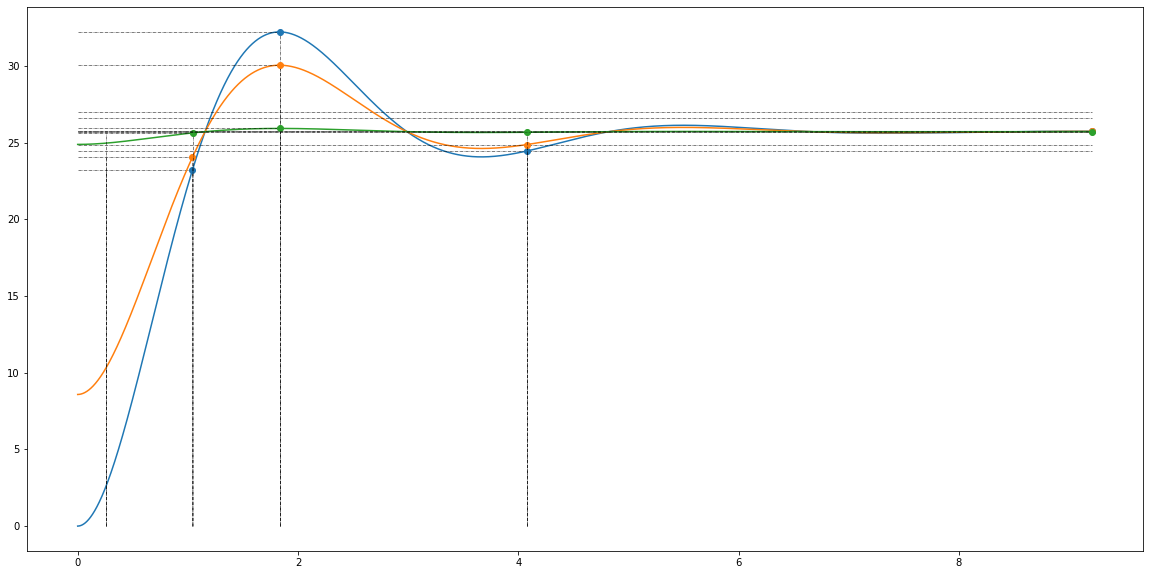
Comparez avec un saut de consigne de 0° à 30°, de 10° à 30° et de 29° à 30°.
# Création de la fenêtre à une taille donnée
fig = plt.figure("Steps comparaison",figsize=(20,10))
ax = fig.subplots()
# Saut de 0° à 30°
warnings.filterwarnings('ignore') # Pour éviter d'afficher un message d'erreur inutile
peak, peakTime, yout, t = rlf.stepFromTo(G_BF, 0, 30, focus=True, NameOfFigure="Steps comparaison")
warnings.resetwarnings() # Pour réactiver l'affichage d'erreurs
info = rlf.step_info(yout, t)
rlf.printInfo(info)
print("")
# Saut de 10° à 30°
warnings.filterwarnings('ignore') # Pour éviter d'afficher un message d'erreur inutile
peak, peakTime, yout, t = rlf.stepFromTo(G_BF, 10, 30, focus=True, NameOfFigure="Steps comparaison")
warnings.resetwarnings() # Pour réactiver l'affichage d'erreurs
info = rlf.step_info(yout, t)
rlf.printInfo(info)
print("")
# Saut de 29° à 30°
warnings.filterwarnings('ignore') # Pour éviter d'afficher un message d'erreur inutile
peak, peakTime, yout, t = rlf.stepFromTo(G_BF, 29, 30, focus=True, NameOfFigure="Steps comparaison")
warnings.resetwarnings() # Pour réactiver l'affichage d'erreurs
info = rlf.step_info(yout, t)
rlf.printInfo(info)
print("")
DCGain : 25.740792643479445
Overshoot : 25.161344614625737
Peak : 32.21752218704154
PeakTime : 1.8328577340232597
RiseTime : 0.7847209996923704
SettlingTime : 4.076496648636657
DCGain : 25.73194794895096
Overshoot : 16.771343960105977
Peak : 30.04754144710496
PeakTime : 1.8328577340232597
RiseTime : 0.7847209996923704
SettlingTime : 4.076496648636657
DCGain : 25.715143029346976
Overshoot : 0.8144423371035048
Peak : 25.9245780412247
PeakTime : 1.8328577340232597
RiseTime : 0.7847209996923705
SettlingTime : 4.078338716711053
Diagrammes fréquentiels¶
Représentez le système modélisé par un pôle simple \( H_{BO}(p)=\frac{1}{p+1} \) dans les différents diagrammes pour visualiser l’effet d’un pôle : p=-1, \(\tau\)=1s et \(\omega_n\)=1rad/s
H_BO = ml.tf(1, [1, 1])
Nyquist (cf. p. 4-6)¶
Afin de tracer le diagramme de Nyquist, il suffit d’entrer la ligne de code suivante:
real, imag, freq = ml.nyquist(H_BO);
plt.axis('equal')
(-1.1, 1.1, -0.5499985390608296, 0.5499985390608296)
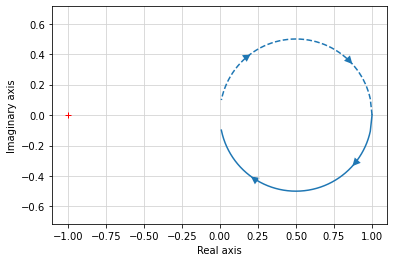
Attention
Attention, le graphique est tracé aussi pour des \(\omega_n<0\) (en trait discontinu) ce qui n’a aucun sens physiquement! Il ne faut donc tenir compte que du tracé en trait plein.
Note
La commande plt.axis('equal') a pour but de modifier les échelles des axes du graphe afin qu’elles soient les mêmes et ainsi faciliter la compréhension en évitant de déformer le tracé (ellipse au lieu d’un cercle).
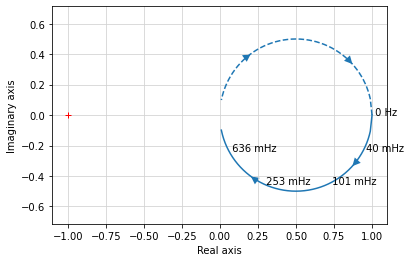
On peut également demander à python d’afficher les fréquences sur le graphe:
ml.nyquist(H_BO, label_freq=200);
plt.axis('equal')
(-1.1, 1.1, -0.5499985390608296, 0.5499985390608296)
Bode (cf. p. 4-7 à 4-12)¶
Pour tracer le diagramme de Bode, on peut soit laisser python fixer automatiquement la plage de variation de la pulsation:
ml.bode(H_BO);
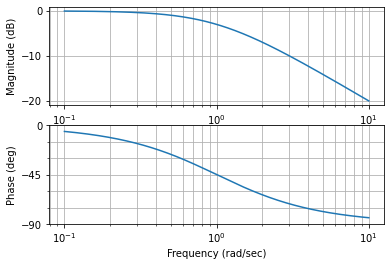
soit imposer l’intervalle de variation de la pulsation en faisant ainsi:
w = np.logspace(-2, 2, 10000) # Echelle logarithmique allant de 10^-2 à 10^2
ml.bode(H_BO, w);
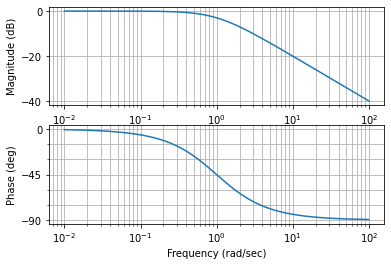
La différence entre les 2 solutions est le nombre de points de calculs (= points d’affichage)
À faire
Comparez la courbe réelle à son tracé asymptotique (voir pages 4-11 et 12).
Nichols (cf. p. 4-18)¶
On peut soit utiliser la fonction nichols du package python Control et on obtient ceci:
ml.nichols(H_BO)
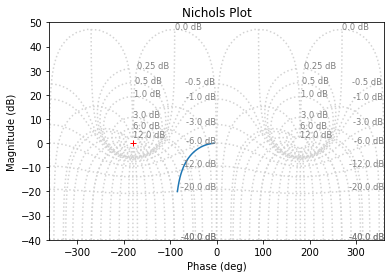
Ou on utilise la fonction nichols revue dans le package ReguLabFct pour faciliter sa lecture dans le cadre du laboratoire de régulation:
rlf.nichols(H_BO)
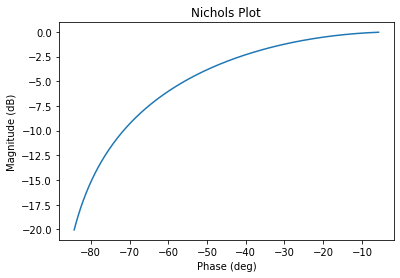
Résumé sur l’effet d’un pôle (cf. p. 4-16)¶
Module: \(\left\{ \begin{array}{ll} \omega<\omega_c : rien\\ \omega>\omega_c : -20dB/décade \end{array} \right.\)
Phase: \(\left\{ \begin{array}{ll} \omega<\omega_c : rien\\ \omega>\omega_c : -90° \end{array} \right.\)
Effet d’une modification du gain statique sur les différents diagrammes¶
Observez l’effet du gain statique : K=2, 5, 10 …
Tracez les 3 graphiques:
K_list = [2, 5, 10]
for K in K_list:
fig_nyquist = plt.figure("Nyquist",figsize=(20,10))
ml.nyquist(K*H_BO, label_freq=200)
fig_bode = plt.figure("Bode",figsize=(20,10))
ml.bode(K*H_BO)
fig_nichols = plt.figure("Nichols",figsize=(20,10))
rlf.nichols(K*H_BO, NameOfFigure="Nichols", labels=[str(K)])
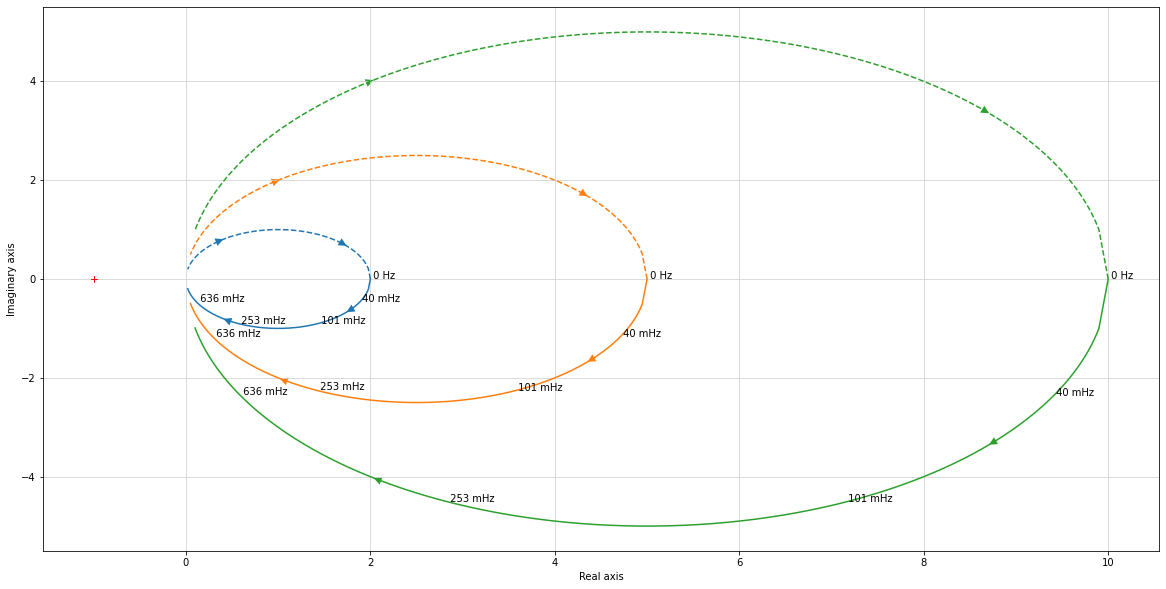
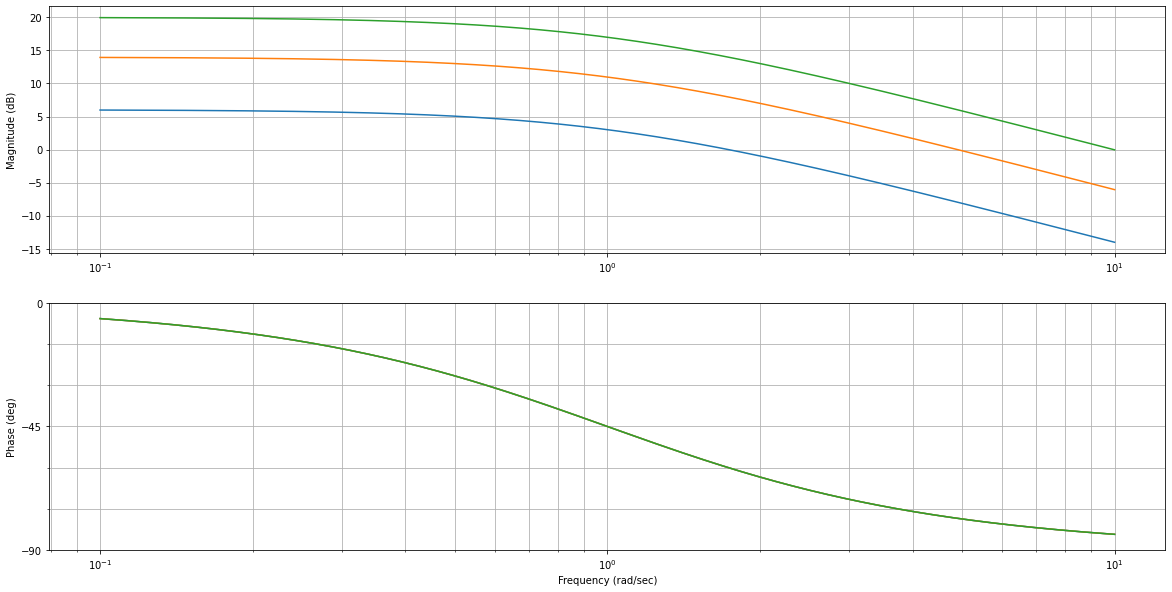
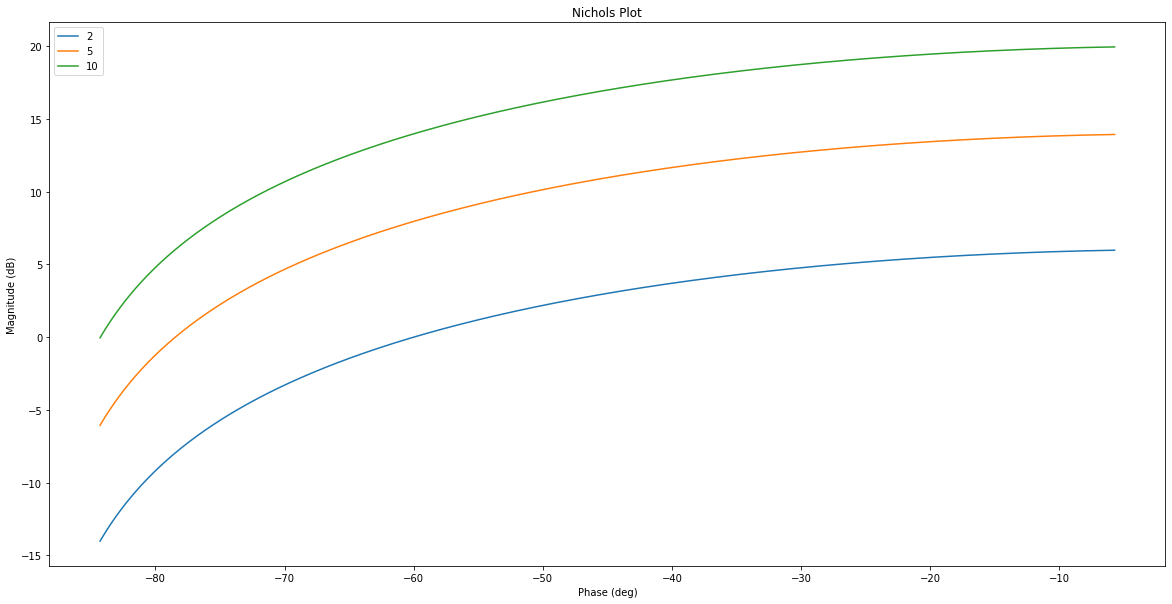
Concluez sur l’effet d’une augmentation de constante (cf. augmentation du gain proportionnel en BO) :
Effet dans:
Nyquist : …
Bode : …
Nichols : …
Nyquist : Étalement suivant l’axe des réels
Bode: Translation verticale du gain de 20log(K) et phase indépendante de K
Nichols: Translation verticale de la courbe de 20log(K)
Car \( \begin{alignat*}{2} K*H\Rightarrow \left\{ \begin{aligned} \begin{array}{ll} M_{dB} = 20*\log(K*H) = 20\log(H)+20\log(K) = 20\log(H) + translation\\ \varphi = \varphi(K)+\varphi(H)=0^{\circ}+\varphi(H) \end{array} \end{aligned}\right. \end{alignat*}\ \)
Danger
Attention que l’analyse fréquentielle s’applique sur le système en boucle ouverte contrairement à l’analyse temporelle (\(\rightarrow\) réponse indicielle) qui s’applique, elle, sur le système en boucle fermée!
