Séance 6¶

Objectifs de la séance¶

Résolution graphique de la détermination d’un correcteur PD
Résolution graphique de la détermination d’un correcteur PID

Régulateur PD¶

Exercice 6 page 7-15 (fait au cours)¶

Soit la fonction de boucle ouverte d’un processus:

\[G(p)={\frac {1}{p(1+0,1p)(1+p)}}\]

On demande de déterminer graphiquement le correcteur PD de manière à optimiser le temps de réponse du système, à garantir une erreur de vitesse de 10% et une marge de phase de 45°.

Solution:¶

Fixer l’erreur de vitesse à 10% impose le gain: \(\varepsilon_v={\frac{1}{K_P}}=0.1\) d’où \(K_P=10\) puisque le système est de classe 1 (cf. p. 6-3).

# Fonction de transfert en boucle ouverte
G1 = ml.tf(1, [1, 0])
G2 = ml.tf(1, [0.1, 1])
G3 = ml.tf(1, [1, 1])
G = G1*G2*G3  # G de l'énoncé 

MP = 45 # Marge de phase réclamée
Kp = 10

Pour choisir la constante de temps de dérivation, nous avons deux possibilités:

Compensation du pôle dominant
Placement fréquentiel

\(1^{ère}\) méthode: Compensation du pôle dominant¶

\(\tau_d=1\) et nous vérifions les performances obtenues pour le système corrigé.

tD = 1
Corr = Kp*ml.tf([tD, 1],1)

fig = plt.figure("Nichols",figsize=(20,10))
ax = fig.subplots()
rlf.nichols(G, grid = False, labels=['G(p)'], NameOfFigure = "Nichols")
rlf.nichols(Kp*G, grid = False, labels=['10*G(p)'], NameOfFigure = "Nichols", linestyle = '-.')
rlf.nichols(Corr*G, grid = False, labels=['10*(1+p)*G(p)'], NameOfFigure = "Nichols", linestyle = '--')

ax.plot(-180+MP, 0,'k+'); # ; pour supprimer les lignes de sortie matplotlib

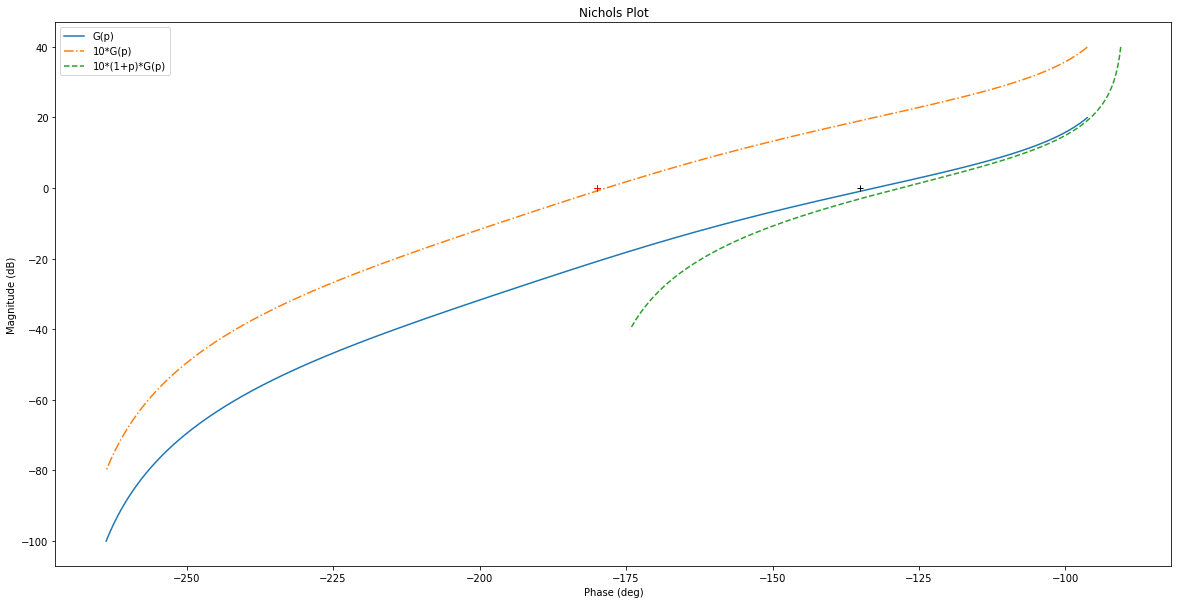
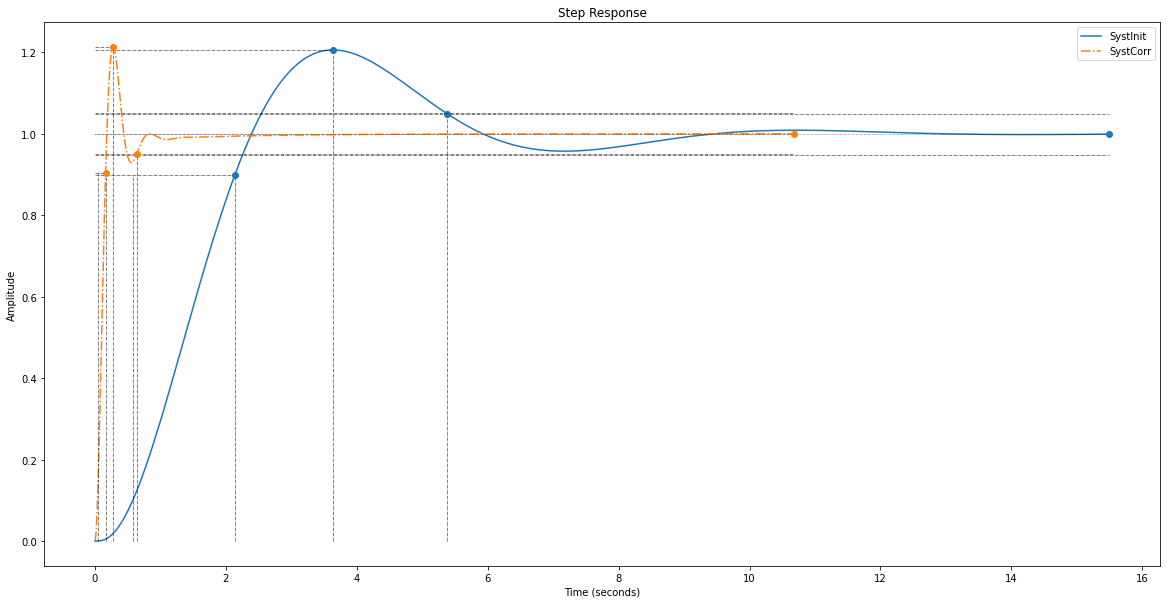
Les performances du système ainsi corrigé sont :

fig = plt.figure("Step Response",figsize=(20,10))

# Système non corrigé
# -------------------

Gbf = ml.feedback(G,1)
info = rlf.stepWithInfo(Gbf, NameOfFigure="Step Response", sysName='SystInit') # Renvoie toutes les infos du step

ep = (1-info.DCGain)*100 # Erreur de position

gm, pm, wg, wp = ml.margin(G) # Extract the gain margin (Gm) and the phase margin (Pm)

print("\nSystème non corrigé")
print("-------------------")
rlf.printInfo(info)

# Système corrigé
# ---------------
Gbf_PD = ml.feedback(Corr*G,1)
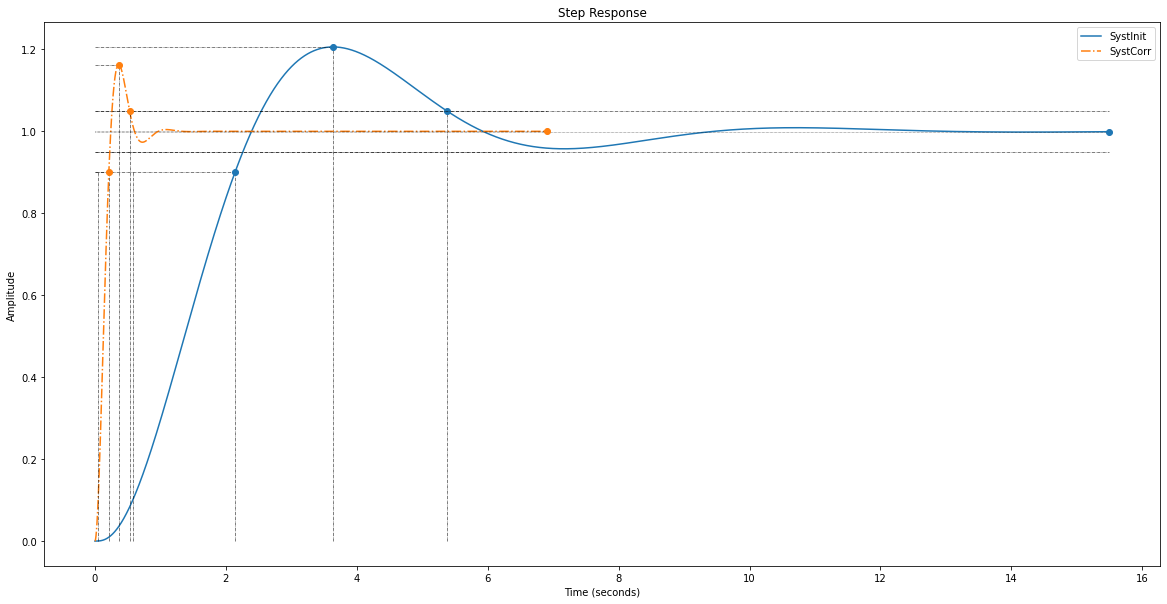
info_PD = rlf.stepWithInfo(Gbf_PD, NameOfFigure="Step Response", sysName='SystCorr', linestyle='-.') # Renvoie toutes les infos du step

ep_PD = (1-info_PD.DCGain)*100 # Erreur de position

gm, pm, wg, wp = ml.margin(Corr*G) # Extract the gain margin (Gm) and the phase margin (Pm)

print("\nSystème corrigé")
print("---------------")
rlf.printInfo(info_PD)

Système non corrigé
-------------------
DCGain : 0.9990781353815176
Overshoot : 20.711775188004733
Peak : 1.2060049527342471
PeakTime : 3.636378059961078
RiseTime : 1.5608835065561832
SettlingTime : 5.383265559354145

Système corrigé
---------------
DCGain : 0.9999999999999946
Overshoot : 16.303349881758788
Peak : 1.1630334988175817
PeakTime : 0.3626934214887108
RiseTime : 0.16373017312918947
SettlingTime : 0.5284961284549786

\(2^{ème}\) méthode: placement fréquentiel¶

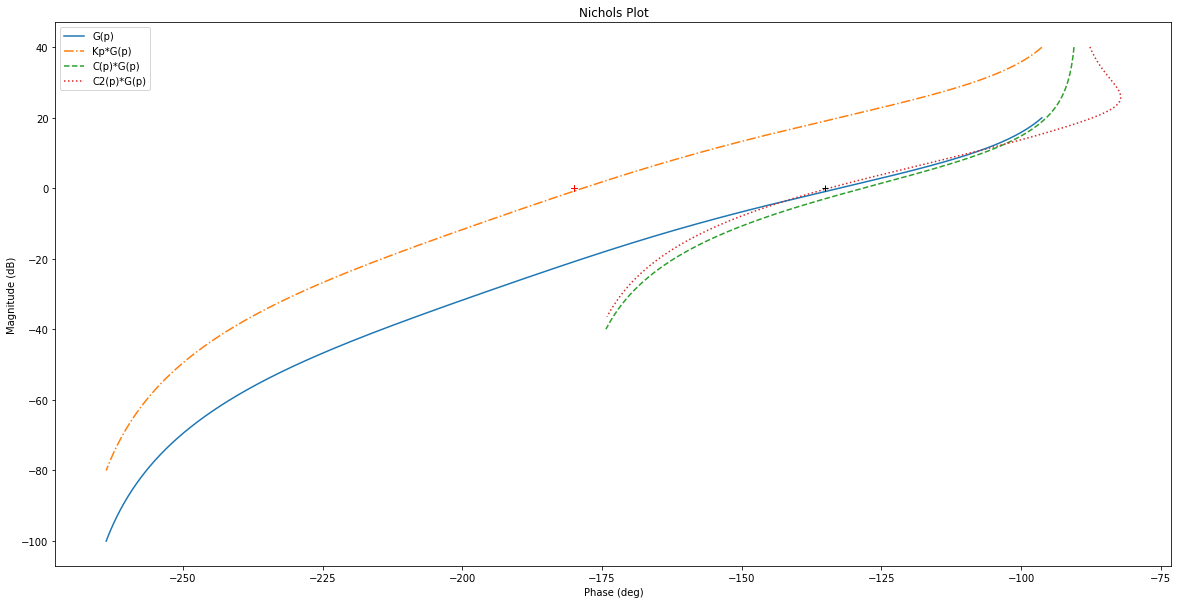
\(K_P\) étant fixé, traçons \(K_P*G(p)\) : le système est instable et nous allons nous efforcer de le stabiliser par l’intermédiaire du terme \((1+\tau_D*p)\).

Ce terme a pour effet, pour la pulsation \(\omega=\frac{10}{\tau_D}\), de translater le module de +20 dB et d’introduire un déphasage de +90° (+84° pour être précis).

Comme nous voulons que le système en trait mixte soit corrigé et passe par le point (0dB,-135°), cherchons le point qui a une phase de –135°-84° ; son module vaut -23 dB. Il sera donc corrigé par le terme \((1+\tau_D*p)\) et passera approximativement par le point voulu (0dB,-135°).

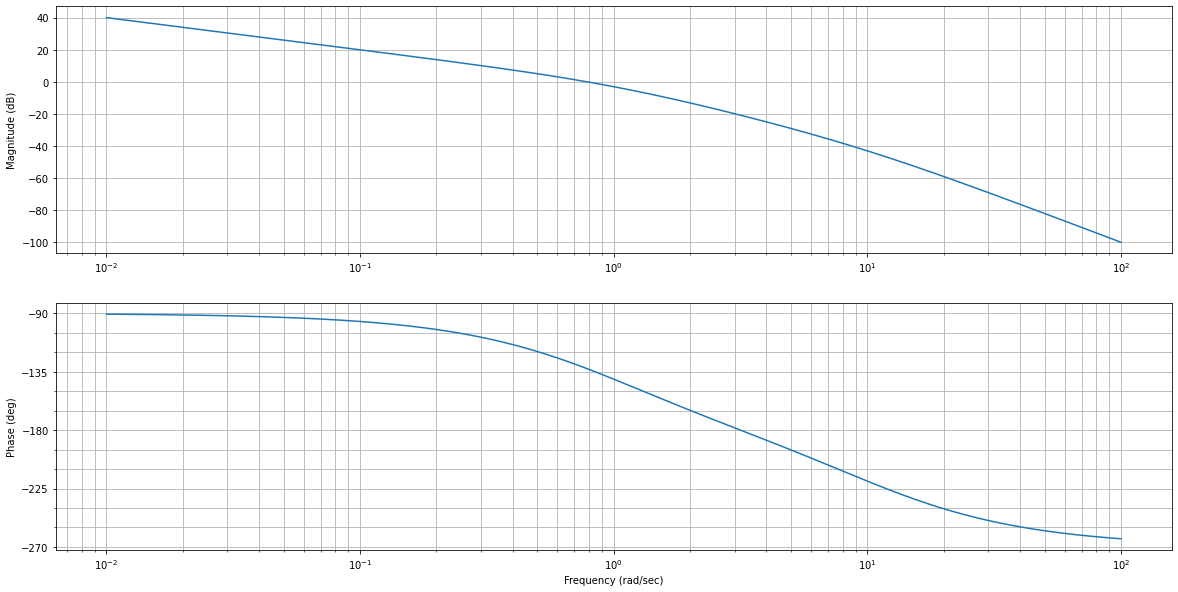
Sur la courbe en trait interrompu, le point (–23dB,–135°-84°) correspond à une pulsation de 9.9rad/s, soit : \(\tau_D=\frac{10}{\omega_{à -135°-84°}}=\frac{10}{9.9}=1.01s\).

# Lecture phase
fig = plt.figure("Bode",figsize=(20,10))
mag, w = rlf.getValues(G, -180+MP-84, printValue=True, NameOfFigure="Bode")

# tD
tD = 10/w # = tD conseillé
print(f"tau_D = {tD:.2f}")
Corr = Kp*ml.tf([tD, 1],1)

fig = plt.figure("Nichols",figsize=(20,10))
ax = fig.subplots()
rlf.nichols(G, grid = False, labels=['G(p)'], NameOfFigure = "Nichols")
rlf.nichols(Kp*G, grid = False, labels=['Kp*G(p)'], NameOfFigure = "Nichols", linestyle = '-.')
rlf.nichols(Corr*G, grid = False, labels=['C(p)*G(p)'], NameOfFigure = "Nichols", linestyle = '--')

ax.plot(-180+MP, 0,'k+'); # Ajout du repère (+) par lequel on est censé passer

gm, pm, wg, wp = ml.margin(Corr*G) # Extrait la marge de gain (Gm) et de phase (Pm)
print(f"Le système ainsi corrigé présente une marge de phase de {pm:.2f}° et une marge de gain de {gm:.2f} dB.")

Gain à -219° = -42.869391796777016 dB
Fréquence à -219° = 9.91515778991914 rad/sec
tau_D = 1.01
Le système ainsi corrigé présente une marge de phase de 51.72° et une marge de gain de inf dB.

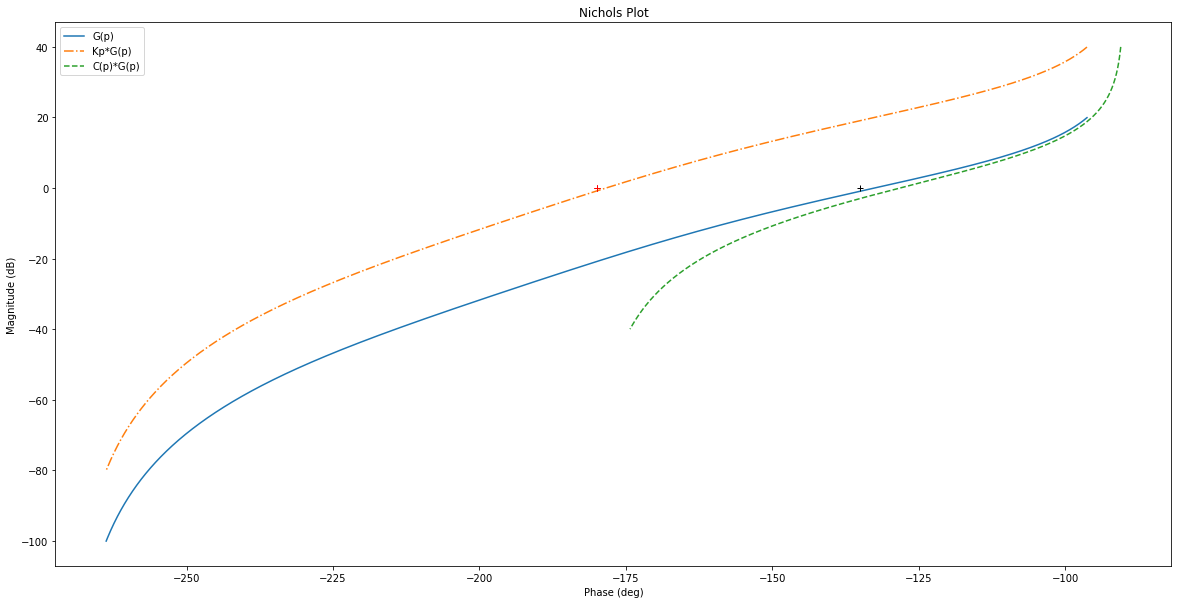
La marge de phase étant malgré tout toujours trop grande, par essai et erreur, nous allons augmenter \(\tau_D\).

tD = 15/w # tD trouvé par essais-erreurs
print(f"tau_D = {tD:.2f}s")
Corr2 = Kp*ml.tf([tD, 1],1)

fig = plt.figure("Nichols",figsize=(20,10))
ax = fig.subplots()
rlf.nichols(G, grid = False, labels=['G(p)'], NameOfFigure = "Nichols")
rlf.nichols(Kp*G, grid = False, labels=['Kp*G(p)'], NameOfFigure = "Nichols", linestyle = '-.')
rlf.nichols(Corr*G, grid = False, labels=['C(p)*G(p)'], NameOfFigure = "Nichols", linestyle = '--')
rlf.nichols(Corr2*G, grid = False, labels=['C2(p)*G(p)'], NameOfFigure = "Nichols", linestyle = ':')

ax.plot(-180+MP, 0,'k+'); # Ajout du repère (+) par lequel on est censé passer

gm, pm, wg, wp = ml.margin(Corr2*G) # Extrait la marge de gain (Gm) et de phase (Pm)
print(f"Le système ainsi corrigé présente une marge de phase de {pm:.2f}° et une marge de gain de {gm:.2f} dB.")

tau_D = 1.51s
Le système ainsi corrigé présente une marge de phase de 45.62° et une marge de gain de inf dB.

Les performances du système ainsi corrigé sont :

import warnings
warnings.filterwarnings("ignore", category=PendingDeprecationWarning) # Pour ignorer des message d'avertissement inutiles

# Système non corrigé
# -------------------

Gbf = ml.feedback(G,1)
fig = plt.figure("Step Response",figsize=(20,10))
info = rlf.stepWithInfo(Gbf, NameOfFigure="Step Response", sysName='SystInit') # Renvoie toutes les infos du step

ep = (1-info.DCGain)*100 # Erreur de position

gm, pm, wg, wp = ml.margin(G) # Extract the gain margin (Gm) and the phase margin (Pm)

print("\nSystème non corrigé")
print("-------------------")
rlf.printInfo(info)

# Système corrigé
# ---------------
Gbf_PD = ml.feedback(Corr2*G,1)
info_PD = rlf.stepWithInfo(Gbf_PD, NameOfFigure="Step Response", sysName='SystCorr', linestyle='-.') # Renvoie toutes les infos du step

ep_PD = (1-info_PD.DCGain)*100 # Erreur de position

gm, pm, wg, wp = ml.margin(Corr2*G) # Extract the gain margin (Gm) and the phase margin (Pm)

print("\nSystème corrigé")
print("---------------")
rlf.printInfo(info_PD)

Système non corrigé
-------------------
DCGain : 0.9990781353815176
Overshoot : 20.711775188004733
Peak : 1.2060049527342471
PeakTime : 3.636378059961078
RiseTime : 1.5608835065561832
SettlingTime : 5.383265559354145

Système corrigé
---------------
DCGain : 0.9999777307492984
Overshoot : 21.339622232529877
Peak : 1.2133692009006234
PeakTime : 0.2787350938997571
RiseTime : 0.12281431340410752
SettlingTime : 0.636498528598679

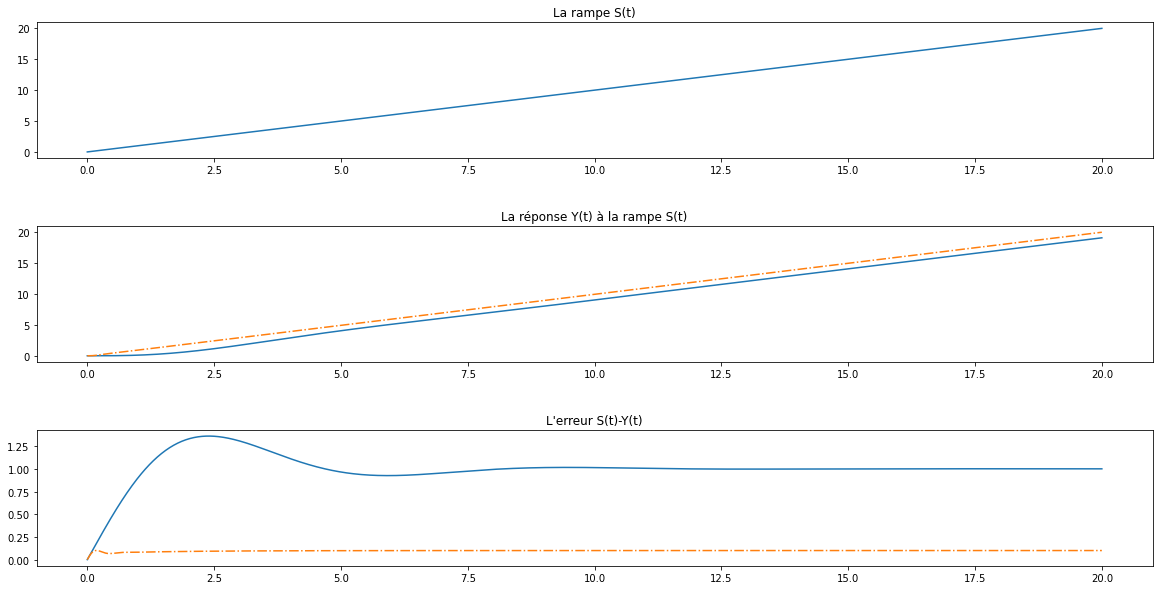
# Mesure de l'erreur de vitesse
t = np.linspace(0, 20, 1000)
s = t
warnings.filterwarnings('ignore') # Pour désactiver les warnings inutiles
[y, t, xout] = ml.lsim(Gbf,s,t) # Simuler la réponse à une rampe => erreur de vitesse
[y2, t, xout2] = ml.lsim(Gbf_PD,s,t) # Simuler la réponse à une rampe => erreur de vitesse
warnings.filterwarnings('default') # Pour réactiver les warnings

plt.figure("Erreur de vitesse",figsize=(20,10))
plt.subplot(3,1,1); plt.plot(t,s); plt.title("La rampe S(t)")
plt.subplot(3,1,2); plt.plot(t,y); plt.plot(t, y2, linestyle='-.'); plt.title("La réponse Y(t) à la rampe S(t)")
plt.subplot(3,1,3); plt.plot(t,(s-y)); plt.plot(t, (s-y2), linestyle='-.'); plt.title("L'erreur S(t)-Y(t)")
plt.subplots_adjust(hspace=0.5) # Pour laisser un peu d'espace pour les titres

ev = s[-1] - y[-1] # Erreur de vitesse système original
ev2 = s[-1] - y2[-1] # Erreur de vitesse du système corrigé

print(f"L'erreur de vitesse du système original vaut {ev*100:.1f}% et celle du système corrigé vaut {ev2*100:.1f}%.")

L'erreur de vitesse du système original vaut 100.0% et celle du système corrigé vaut 10.0%.

Régulateur PID¶

Soit le système asservi à retour unitaire dont la fonction de boucle ouverte est :

\[ H(p)=\frac{20}{(5+p)(2p+3)(4+3p)} \]

On demande de déterminer le correcteur dont le but est de permettre une erreur statique nulle et une erreur de vitesse minimale, tout en assurant une réponse indicielle dont le dépassement est limité à 5%.

Stratégie de dimensionnement du correcteur adéquat

Puisqu’on cherche à avoir une erreur statique nulle, la théorie nous dit que le système doit être au moins de classe 1 (cf. p. 6-3). Or, il n’y a pas de pôle à l’origine ( = nous ne pouvons pas mettre de pôle en évidence) donc nous sommes avec un système de classe 0. Il faut dès lors augmenter la classe de notre système, ce qui peut se faire en intégrant ce dernier.

L’erreur de vitesse devant être minimale, il faudra fixer un K le plus grand possible vu qu’on obtient un système de classe 1 après l’avoir intégré et que l’erreur de vitesse est égale à \(\frac{1}{K}\) dans ce cas.

Enfin, on doit limiter le dépassement à 5%, ce qui limitera notre K. Le problème est qu’on se retrouve avec un système d’ordre 3 à condition d’utiliser la technique de compensation du pôle dominant pour dimensionner \(\tau_I\). Les pôles n’étant pas si différents, nous ne pouvons pas nous permettre de simplifier le système à un système du second ordre et nous devons donc ajouter un correcteur D par compensation du pôle dominant afin de réduire l’ordre de notre système et ainsi retrouver un système d’ordre 2 dont on connaît la forme canonique et pour lequel nous pouvons donc exploiter la technique de l’identifiaction pour fixer K.

Dimensionnement du correcteur

En mettant la fonction de transfert sous forme canonique, on obtient:

\[ H(p)=\frac{\frac{1}{3}}{(\frac{1}{5}p+1)(\frac{2}{3}p+1)(\frac{3}{4}p+1)} \]

Le pôle dominant étant celui lié à la constante de temps \(\tau\) la plus grande, nous dimensionnons \(\tau_I=\frac{3}{4}\)
Le second pôle dominant nous donne \(\tau_D=\frac{2}{3}\)
Nous obtenons donc le correcteur PID suivant:

\[ C(p)=K_P*\frac{(\frac{2}{3}p+1)*(\frac{3}{4}p+1)}{p} \]

Ce qui nous donne comme fonction de transfert pour la boucle ouverte:

\[ G_{BO}(p) = \frac{K_P*\frac{1}{3}}{p*(\frac{1}{5}p+1)} = \frac{\frac{K_P}{3}}{\frac{1}{5}p^2+p} \]
La boucle fermée étant à retour unitaire, on obtient:

\[ G_{BF}(p) = \frac{\frac{K_P}{3}}{\frac{1}{5}p^2+p+\frac{K_P}{3}} = \frac{1}{\frac{3}{5K_P}*p^2+\frac{3}{K_P}*p+1} \]

Par identification, on trouve:

\[\begin{split} \begin{alignat*}{2} \left\{ \begin{aligned} \begin{array}{ll} \frac{2\zeta}{\omega_n} = \frac{3}{K_P} \\ \frac{1}{\omega_n^2} = \frac{3}{5K_P} \end{array} \end{aligned}\right. \end{alignat*}\ \end{split}\]

Or,

\[ D_p=100*e^{-\frac{k\pi\zeta}{\sqrt{1-\zeta^2}}} \Rightarrow 5 = 100*e^{-\frac{\pi\zeta}{\sqrt{1-\zeta^2}}} \Rightarrow \zeta=0.69 \]

Ce qui nous permet de trouver:

\[\begin{split} \left\{ \begin{aligned} \begin{array}{ll} K_P = 7.876 \\ \omega_n = 3.623 rad/s \end{array} \end{aligned}\right. \end{split}\]
Le correcteur PID qui permet d’assurer un erreur statique nulle, une erreur de vitesse minimum et un dépassement de 5% pour le système donné est donc:

\[ C(p)=5.906*\frac{(\frac{2}{3}p+1)*(\frac{3}{4}p+1)}{\frac{3}{4}p} \]

import warnings
warnings.filterwarnings("ignore", category=PendingDeprecationWarning) # Pour ignorer des message d'avertissement inutiles

# ------------------------
# Configuration du système
# ------------------------

# Système initial
num = 20
H1 = ml.tf(1, [1, 5])
H2 = ml.tf(1, [2, 3])
H3 = ml.tf(1, [3, 4])
H = num*H1*H2*H3  # H de l'énoncé
G_BF_init = ml.feedback(H, 1)

# Correcteur
Kp = 7.876
tI = 3/4
tD = 2/3
C = Kp*ml.tf([tI, 1],[1, 0])*ml.tf([tD, 1],[1])

# Système corrigé
G_BO = C*H
G_BF = ml.feedback(G_BO, 1)

# ------------------
# Analyse du système
# ------------------

# Step
fig = plt.figure("Step Response",figsize=(20,10))
info = rlf.stepWithInfo(G_BF_init, NameOfFigure="Step Response", sysName='Système initial')
info_PID = rlf.stepWithInfo(G_BF, NameOfFigure="Step Response", sysName='Système corrigé')

# Erreurs statiques
e0_init = 1-info.DCGain
e0 = 1-info_PID.DCGain
print(f"\nL'erreur de position du système original vaut {e0_init*100:.1f}% et celle du système corrigé vaut {e0*100:.1f}%.")

# Dépassements
print(f"\nLe dépassement du système original vaut {info.Overshoot:.1f}% et celui du système corrigé vaut {info_PID.Overshoot:.1f}%.")

# Erreurs de vitesse
t = np.linspace(0, 20, 1000)
s = t
warnings.filterwarnings('ignore') # Pour désactiver les warnings inutiles
[y, t, xout] = ml.lsim(G_BF_init,s,t) # Simuler la réponse à une rampe => erreur de vitesse
[y2, t, xout2] = ml.lsim(G_BF,s,t) # Simuler la réponse à une rampe => erreur de vitesse
warnings.filterwarnings('default') # Pour réactiver les warnings

plt.figure("Erreur de vitesse",figsize=(20,10))
plt.subplot(3,1,1); plt.plot(t,s); plt.title("La rampe S(t)")
plt.subplot(3,1,2); plt.plot(t,y); plt.plot(t, y2); plt.title("La réponse Y(t) à la rampe S(t)")
plt.subplot(3,1,3); plt.plot(t,(s-y)); plt.plot(t, (s-y2)); plt.title("L'erreur S(t)-Y(t)")
plt.subplots_adjust(hspace=0.5) # Pour laisser un peu d'espace pour les titres

ev = s[-1] - y[-1] # Erreur de vitesse système original
ev2 = s[-1] - y2[-1] # Erreur de vitesse du système corrigé

print(f"\nL'erreur de vitesse du système original vaut {ev*100:.1f}% et celle du système corrigé vaut {ev2*100:.1f}%.")

# Nichols (pas nécessaire ici mais toujours intéressant à observer)
fig = plt.figure("Nichols",figsize=(20,10))
frequencies = np.linspace(10**-5, 10**5, 10**6) # Pour bien voir vers où on converge dans les hautes fréquences (jusqu'à 10^5 rad/s ici)
rlf.nichols(H, grid = False, labels=['Système initial'], NameOfFigure = "Nichols", omega=frequencies)
rlf.nichols(G_BO, grid = False, labels=['Système corrigé'], NameOfFigure = "Nichols", omega=frequencies)

L'erreur de position du système original vaut 75.0% et celle du système corrigé vaut 0.0%.

Le dépassement du système original vaut 0.9% et celui du système corrigé vaut 5.0%.

L'erreur de vitesse du système original vaut 1530.3% et celle du système corrigé vaut 38.1%.

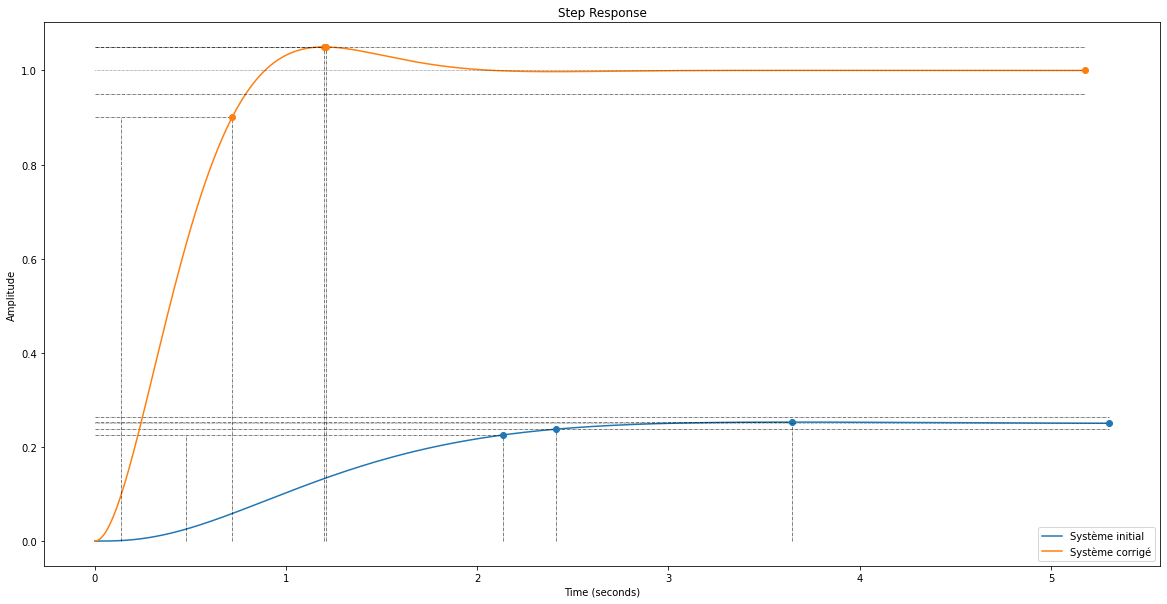
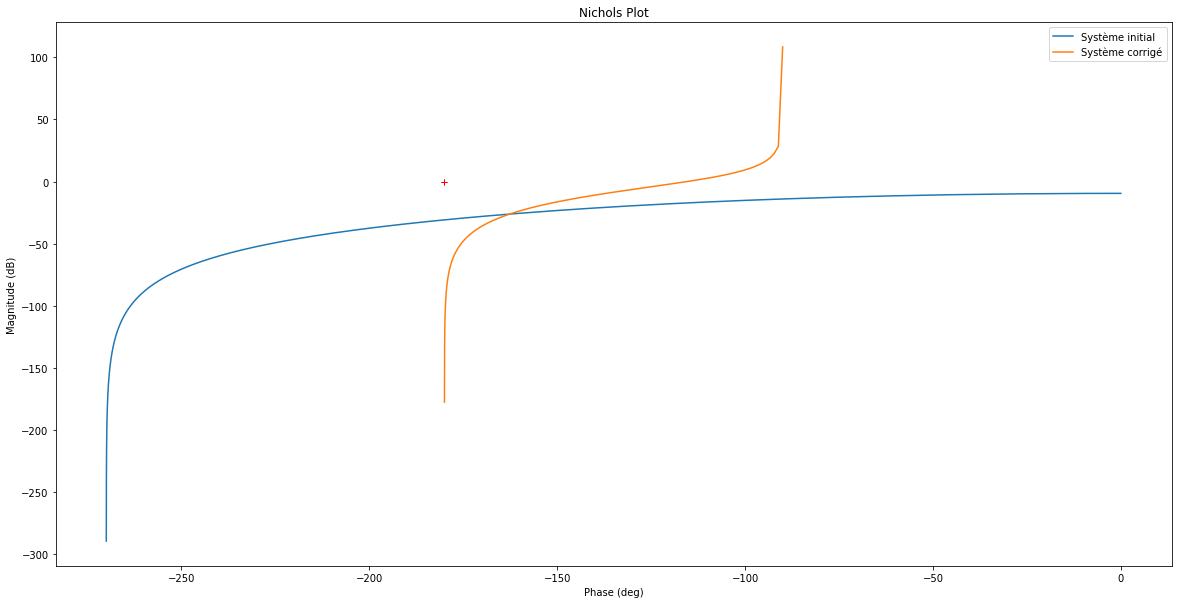
On voit donc bien que l’ajout de notre correcteur PID au système à retour unitaire initial nous permet d’avoir une erreur statique nulle, un dépassement de 5% et une erreur de vitesse limitée (38,1%) alors que ce dernier présentait une erreur statique de 75%, un dépassement de 0.9% et une erreur de vitesse infinie.

Laboratoire de régulation

Séance 6

Contents