Séance 3
Contents
Séance 3¶
Objectifs de la séance¶
Analyse d’un système en boucle fermée : feedback
Analyse de la réponse indicielle et valeurs « idéales » de la réponse à un échelon
Influence du correcteur proportionnel sur les caractéristiques temporelles : dépassement, temps de réponse, … et sur les pôles du système en BF.
Etude d’un système en boucle fermée¶
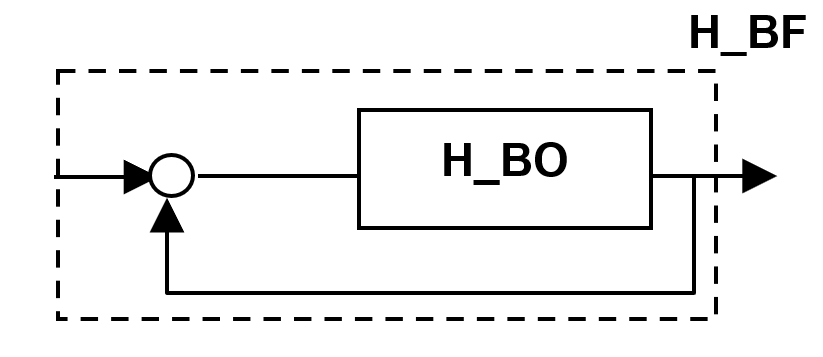
Soit un système en boucle fermée dont la fonction de transfert est :
num = 20
den = [1, 2, 10]
H_BO = ml.tf(num, den)
Pour en déduire la fonction de transfert en boucle fermée, il suffit d’utiliser la fonction feedback qui possède 2 paramètres : la fct de transfert en chaîne directe et celle en chaîne de retour (ici retour unitaire).
H_BF = ml.feedback(H_BO, 1)
print("H_BF =", H_BF)
H_BF =
20
--------------
s^2 + 2 s + 30
Note
Vous pouvez le vérifier en calculant la fonction en BF par la formule de Black.
Identifiez \(\omega_n\) et \(\zeta\):
wn, z, poles = ml.damp(H_BF, doprint=False); # doprint = False afin de ne pas afficher les résultat mais seulement de les stocker.
print("wn = {:.3f} rad/s et zeta = {:.3f}.".format(wn[0], z[0])) # la fonction 'format()' permet de gérer le nombre de décimales qu'on souhaite afficher dans la chaîne de caractères.
wn = 5.477 rad/s et zeta = 0.183.
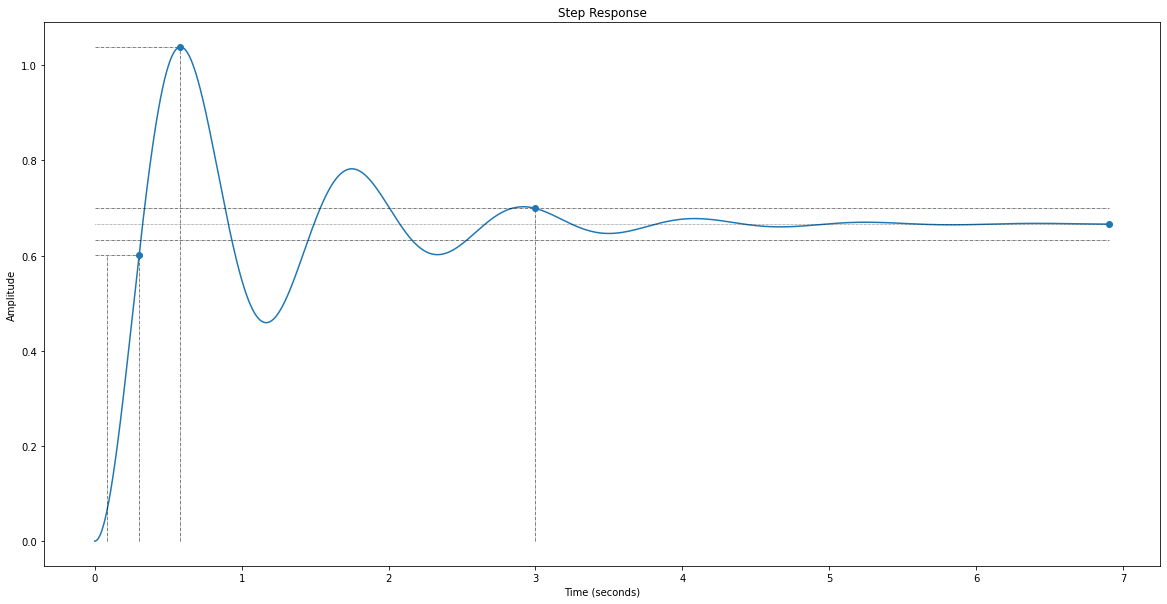
Visualisez les grandeurs caractéristiques de la réponse indicielle en BF :
fig = plt.figure("Step",figsize=(20,10)) # Création de la fenêtre à une taille donnée.
info = rlf.stepWithInfo(H_BF, NameOfFigure="Step") # Traçage de la réponse indicielle et sauvegarde des informations dans l'objet info.
rlf.printInfo(info) # Affiche les informations stockées dans l'objet info.
DCGain : 0.6661408393656921
Overshoot : 55.92386513929972
Peak : 1.038672544010361
PeakTime : 0.5830728528313754
RiseTime : 0.21623436366850776
SettlingTime : 2.997574773027652
Note
Vous pouvez vérifier le gain en régime établi (DCGain):
en mettant la fonction en BF sous forme canonique et en identifiant le numérateur : …
OU en faisant s\(\rightarrow\)0 : …
Comme le système asservi est à retour unitaire, la valeur finale de la réponse (régime permanent) devrait être égale à 1.
L’écart entre la valeur idéale (……) et la valeur réelle (……) permet de qualifier la précision du système. L’écart exprimé en % est appelé erreur de position : \(\varepsilon_0\) ou \(\varepsilon_p\) (cf. Chapitre 6).
Ici \(\varepsilon_0\) = …… %
Astuce
Les informations stockées dans l’objet info sous forme d’attributs sont accessibles en écrivant info.attribut.
Exemple:
info.Overshoot
e_pos = (1 - info.DCGain)*100
print("L'erreur de position vaut ici:", e_pos, "%.")
L'erreur de position vaut ici: 33.385916063430784 %.
Observez la valeur du dépassement en absolu et en relatif :
Absolu = peak = …
Relatif = overshoot = …
Vérifiez que info.Peak correspond à dcgain(H_BF)*(1+info.Overshoot/100)
print("- Le dépassement absolu vaut:", info.Peak)
print("- Le dépassement relatif vaut:", info.Overshoot, "%.")
- Le dépassement absolu vaut: 1.038672544010361
- Le dépassement relatif vaut: 55.92386513929972 %.
Exemple 1 p 3-13¶
Un asservissement de vitesse à retour unitaire possède une fonction de transfert en BO :
1.¶
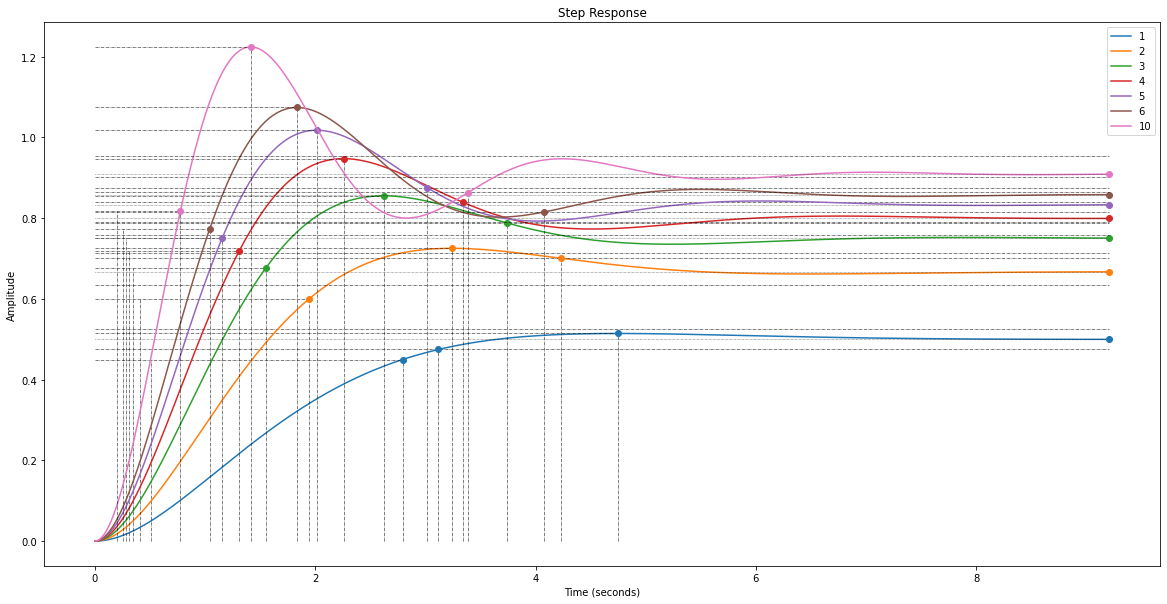
Tracez, pour différentes valeurs de K : 1 2 3 4 5 6 et 10, la réponse indicielle du système en boucle fermée à retour unitaire.
K_values = [1, 2, 3, 4, 5, 6, 10]
# Création de la fenêtre à une taille donnée
fig = plt.figure("Steps",figsize=(20,10))
ax = fig.subplots()
# Réponse indicielle
# Calcule les différentes fonctions de transfert ainsi que la réponse indicielle
infos = []
for K in K_values:
G1 = ml.tf([K], [1, 1]) # Calcul la fonction de transfert en foncion de K
G2 = ml.tf([1], [2, 1])
G_BO = G1*G2
G_BF = ml.feedback(G_BO)
infos.append(rlf.stepWithInfo(G_BF, NameOfFigure='Steps', sysName=K))
# Impression des résultats pour K = 1 et K = 10
print("Les résultats pour K = 1 sont:")
rlf.printInfo(infos[0])
print("\nLes résultats pour K = 10 sont:")
rlf.printInfo(infos[-1]) # -1 pour sélectionner le dernier élément de la liste info.
Les résultats pour K = 1 sont:
DCGain : 0.499616798918951
Overshoot : 2.916419399904391
Peak : 0.5141877201678046
PeakTime : 4.749326428433763
RiseTime : 2.283471725385434
SettlingTime : 3.118933143265462
Les résultats pour K = 10 sont:
DCGain : 0.9088257077904426
Overshoot : 34.672037627934586
Peak : 1.2239340991678875
PeakTime : 1.4139286399623403
RiseTime : 0.5738615913332494
SettlingTime : 3.3879019790107407
Pourquoi insiste-t-on sur le fait qu’il doit être à retour unitaire ?
On insiste sur le fait que le système doit être à retour unitaire afin de directement pouvoir comparer l’entrée ( = consigne) et le sortie de celui-ci.
Observez l’effet sur les grandeurs caractéristiques de la réponse et concluez :
\(\nearrow\) K a pour effet de:
…… l’erreur (\(\varepsilon_0\))
…… la précision (steady state)
…… le temps de montée
…… le dépassement
…… le temps de réponse à 5%
\(\nearrow\) K a pour effet de:
\(\searrow\) l’erreur (\(\varepsilon_0\))
\(\nearrow\) la précision (steady state)
\(\searrow\) le temps de montée
\(\nearrow\) le dépassement
\(\nearrow\) ou \(\searrow\) le temps de réponse à 5% en suivant l’abaque de la page 3-12
Note
K modélise en fait un correcteur P dont vous venez de montrer les principales caractéristiques 🙂
2.¶
Déterminez par essai et erreur la valeur de K pour obtenir une réponse indicielle en BF présentant un dépassement de 20%.
K = ……
\(K \simeq 4.5\)
3.¶
Estimez cette valeur en exploitant les relations et/ou abaques :
On a:
On obtient donc par identification:
Or via l’équation du dépassement (cf. p.3-11), on peut déduire \(\zeta\):
Dès lors, on obtient:
4.¶
Vérifiez les paramètres caractéristiques de la réponse obtenue pour cette valeur de K :
K = 4.4
G1 = ml.tf([K], [1, 1]) # Calcul la fonction de transfert en foncion de K
G2 = ml.tf([1], [2, 1])
G_BO = G1*G2
G_BF = ml.feedback(G_BO)
info = rlf.stepWithInfo(G_BF)
plt.close() # Si on souhaite ne pas afficher le graphe renvoyé par stepWithInfo
print("Dépassement =", info.Overshoot, "%") # \n pour ajouter une ligne vide après
wn, z, __ = ml.damp(G_BF, doprint=False);
print("zeta =", z[0])
print("wn =", wn[0], "rad/s")
Dépassement = 20.07967668512085 %
zeta = 0.4564354645876384
wn = 1.6431676725154984 rad/s
5.¶
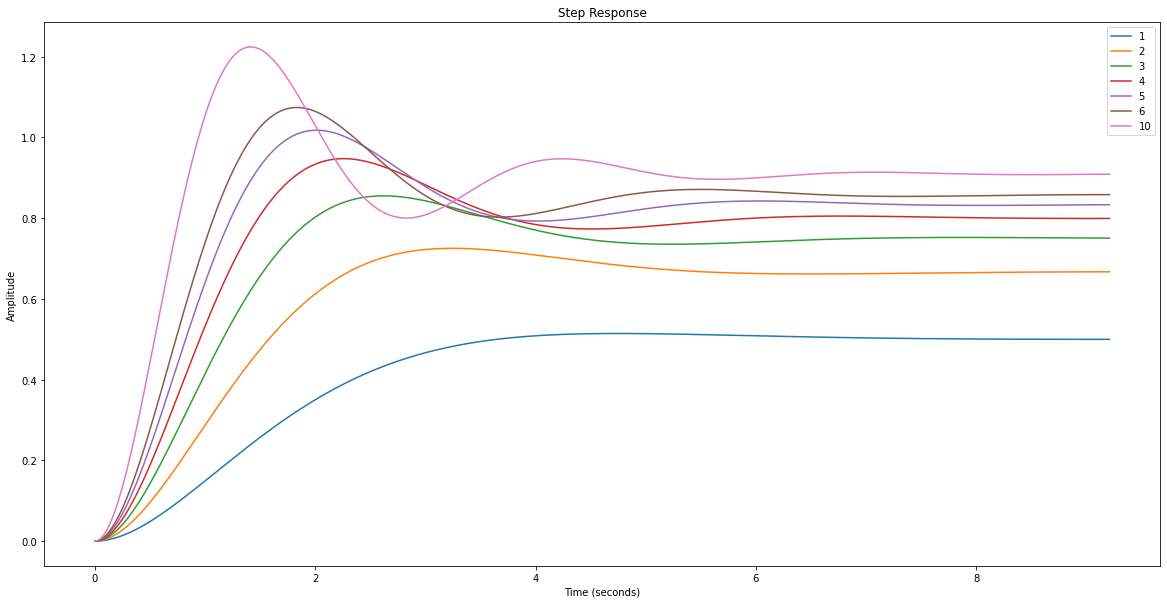
Tracez un diagramme reprenant les différentes réponses indicielles en fonction de K et un diagramme reprenant la position des pôles du système en boucle fermée pour visualiser l’impact de K (un correcteur proportionnel) sur la BF :
K_values = [1, 2, 3, 4, 5, 6, 10]
# %% Réponses indicielles
# Création de la fenêtre à une taille donnée
fig = plt.figure("Steps",figsize=(20,10))
ax = fig.subplots()
# Réponse indicielle
# Calcule les différentes fonctions de transfert ainsi que la réponse indicielle
info = []
for K in K_values:
G1 = ml.tf([K], [1, 1]) # Calcul la fonction de transfert en foncion de K
G2 = ml.tf([1], [2, 1])
G_BO = G1*G2
G_BF = ml.feedback(G_BO)
info.append(rlf.step_(G_BF, NameOfFigure='Steps', sysName=K))
# %% Pôles
# Création de la fenêtre à une taille donnée
fig = plt.figure("Pole Zero Map",figsize=(20,10))
ax = fig.subplots()
# Pour pouvoir boucler sur les couleurs standards afin de directement jouer avec les couleurs des graphes
from itertools import cycle
prop_cycle = plt.rcParams['axes.prop_cycle']
colors = cycle(prop_cycle.by_key()['color'])
# Trace les poles et zéros pour chacune des fonctions de transfert stockées dans 'g'
for K in K_values:
G1 = ml.tf([K], [1, 1]) # Calcul la fonction de transfert en foncion de K
G2 = ml.tf([1], [2, 1])
G_BO = G1*G2
G_BF = ml.feedback(G_BO)
poles, zeros = rlf.pzmap(G_BF, NameOfFigure="Pole Zero Map", sysName=K, color=next(colors));
left, right = plt.xlim() # Stocke les limites gauche et droite du graphe
plt.plot([left, right], [0, 0], 'k:'); # Ligne horizontale passant par 0 pour marquer l'axe des imaginaires

:class: toggle
$p = \sigma \pm j\omega_d$ avec
$
\begin{alignat*}{2}
\left\{ \begin{aligned}
\begin{array}{ll}
\sigma=-\zeta\omega_n \\
\omega_d=\omega_n \sqrt{1-\zeta^2}
\end{array}
\end{aligned}\right.
\Leftrightarrow
\left\{ \begin{aligned}
\begin{array}{ll}
\sigma=cte \\
\omega_d=f(K)
\end{array}
\end{aligned}\right.
\end{alignat*}\
$
Effet d’un correcteur proportionnel de gain A¶
Reprenez l’application 1 d’asservissement de vitesse, le schéma-bloc du système est :

a) Sur un système du \(1^{er}\) ordre¶
On a \(H_m(p)=\frac{31.25}{10.875*10^{-3}*p+1}\) si on néglige l et \(k_{dt}=33*10^{-3}\frac{Vs}{rad}\), soit:
Calculez la fonction de transfert de boucle fermée pour A (1,2,5,9,20,40,60,100, …) :
Par calcul:
Via Python:
A_values = [1,2,5,9,20,40,60,100]
B = 31.25*33*10**(-3)
H_BOs = []
H_BFs = []
for A in A_values:
H_BO = ml.tf(A*B, [10.875e-3, 1])
H_BOs.append(H_BO)
H_BF = ml.feedback(H_BO, 1)
H_BFs.append(H_BF)
print(H_BF)
1.031
-----------------
0.01087 s + 2.031
2.062
-----------------
0.01087 s + 3.062
5.156
-----------------
0.01087 s + 6.156
9.281
-----------------
0.01087 s + 10.28
20.62
-----------------
0.01087 s + 21.62
41.25
-----------------
0.01087 s + 42.25
61.88
-----------------
0.01087 s + 62.88
103.1
-----------------
0.01087 s + 104.1
Quel est l’effet d’une augmentation de A sur:
Le gain statique?
L’erreur de position?
La constante de temps?
# Création de la fenêtre à une taille donnée
fig = plt.figure("Steps with infos",figsize=(20,10))
ax = fig.subplots()
infos = []
for i, H_BF in enumerate(H_BFs):
infos.append(rlf.stepWithInfo(H_BF, NameOfFigure='Steps with infos', sysName=A_values[i]))
print("Le gain statique pour A = 1 vaut", infos[0].DCGain, " et pour A =", A_values[-1],":", infos[-1].DCGain)
print("=> le gain statique se rapproche de 1.\n")
print("L'erreur de position pour A = 1 vaut", 1-infos[0].DCGain, " et pour A =", A_values[-1],":", 1-infos[-1].DCGain)
print("=> L'erreur de position diminue.\n")
print("La constante de temps pour A = 1 vaut", infos[0].SettlingTime/3, "s et pour A =", A_values[-1],":", infos[-1].SettlingTime/3, "s.") # Valeur à 95% de la valeur finale -> 3*tau
print("=> La constante de temps diminue.\n")
print("") # Pour laisser un espace supplémentaire entre les réponses écrites et les graphes
Le gain statique pour A = 1 vaut 0.5071846153845865 et pour A = 100 : 0.9894057623051423
=> le gain statique se rapproche de 1.
L'erreur de position pour A = 1 vaut 0.4928153846154135 et pour A = 100 : 0.010594237694857678
=> L'erreur de position diminue.
La constante de temps pour A = 1 vaut 0.005312531298772257 s et pour A = 100 : 0.00010363581465191978 s.
=> La constante de temps diminue.
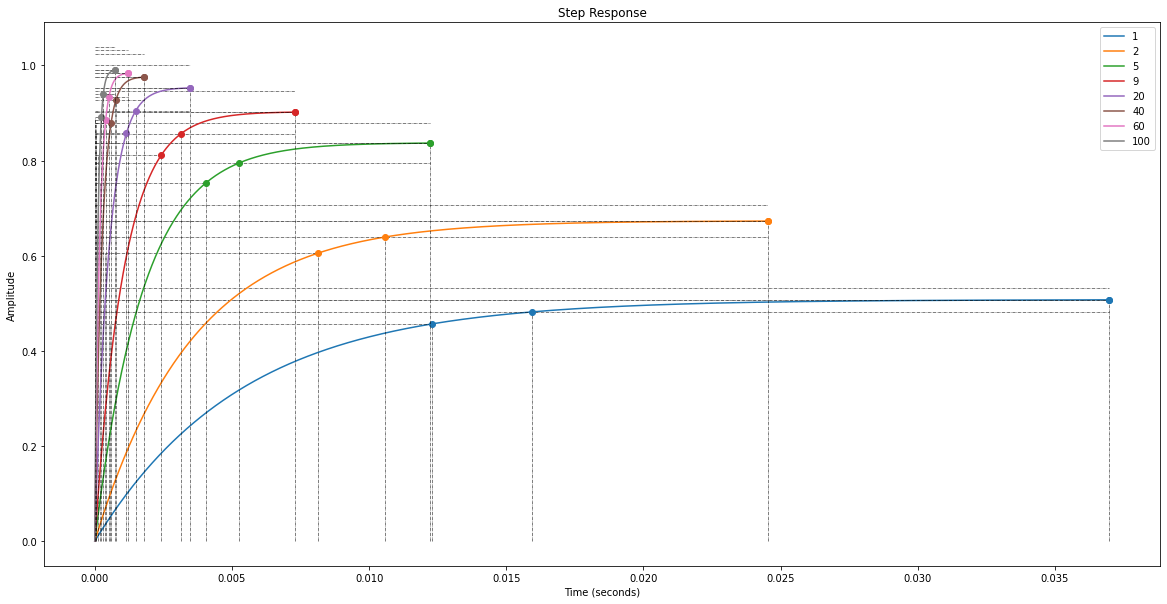
b) Sur un système du \(2^{nd}\) ordre¶
On a \(H_m(p)=\frac{31.25}{1.36*10^{-6}*p^2+10.875*10^{-3}*p+1}\) si on tient compte de l, soit:
Calculez la fonction de transfert de boucle fermée pour ces différentes valeurs de A:
Par calcul:
Via Python:
A_values = [1,2,5,9,20,40,60,100]
B = 1.03125
H_BOs = []
H_BFs = []
for A in A_values:
H_BO = ml.tf(A*B, [1.36e-6, 10.875e-3, 1])
H_BOs.append(H_BO)
H_BF = ml.feedback(H_BO, 1)
H_BFs.append(H_BF)
print(H_BF)
1.031
--------------------------------
1.36e-06 s^2 + 0.01087 s + 2.031
2.062
--------------------------------
1.36e-06 s^2 + 0.01087 s + 3.062
5.156
--------------------------------
1.36e-06 s^2 + 0.01087 s + 6.156
9.281
--------------------------------
1.36e-06 s^2 + 0.01087 s + 10.28
20.62
--------------------------------
1.36e-06 s^2 + 0.01087 s + 21.62
41.25
--------------------------------
1.36e-06 s^2 + 0.01087 s + 42.25
61.88
--------------------------------
1.36e-06 s^2 + 0.01087 s + 62.88
103.1
--------------------------------
1.36e-06 s^2 + 0.01087 s + 104.1
Quel est l’effet d’une augmentation de A sur:
Le gain statique?
L’erreur de position?
# Création de la fenêtre à une taille donnée
fig = plt.figure("Steps with infos",figsize=(20,10))
ax = fig.subplots()
infos = []
for i, H_BF in enumerate(H_BFs):
infos.append(rlf.stepWithInfo(H_BF, NameOfFigure='Steps with infos', sysName=A_values[i]))
print("Le gain statique pour A = 1 vaut", infos[0].DCGain, " et pour A =", A_values[-1],":", infos[-1].DCGain)
print("=> le gain statique se rapproche de 1.\n")
print("L'erreur de position pour A = 1 vaut", 1-infos[0].DCGain, " et pour A =", A_values[-1],":", 1-infos[-1].DCGain)
print("=> L'erreur de position diminue.\n")
print("") # Pour laisser un espace supplémentaire entre les réponses écrites et les graphes
Le gain statique pour A = 1 vaut 0.5071718549900822 et pour A = 100 : 0.9893733591268673
=> le gain statique se rapproche de 1.
L'erreur de position pour A = 1 vaut 0.4928281450099178 et pour A = 100 : 0.010626640873132698
=> L'erreur de position diminue.
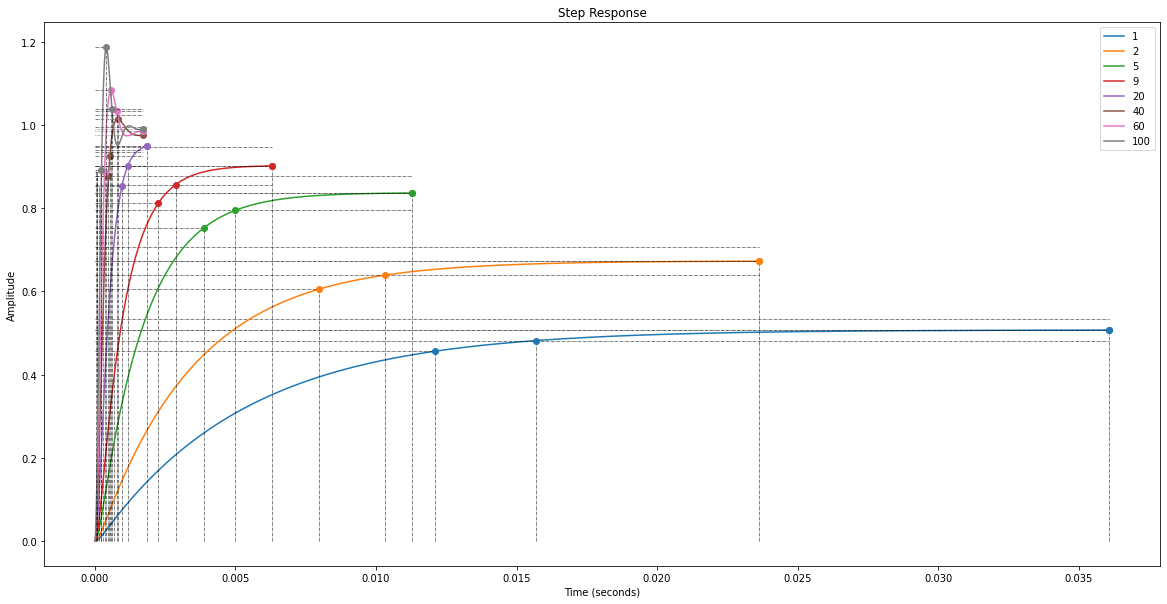
En déduire l’effet d’un correcteur proportionnel sur le régime établi: …
Un correcteur proportionnel a pour effet d’améliorer la précision du système en régime établi.
Quel est l’effet d’une augmentation de A sur:
La pulsation naturelle (\(\omega_n\))?
Le coefficient d’amortissement (\(\zeta\))?
La pseudo pulsation (\(\omega_d\))?
L’amortissement (\(\sigma\))?
Rappel
\( \left. \begin{array}{r} p_1 \\ p_2 \end{array} \right\} = \omega_n*(-\zeta \pm j\sqrt{1-\zeta^2}) = \sigma \pm j\omega_d \) (cf. page 3-7)
# Caractéristiques typiques
# -------------------------
wn_0, z_0, __ = ml.damp(H_BFs[0], doprint=False);
wn_fin, z_fin, __ = ml.damp(H_BFs[-1], doprint=False);
print("La pulsation naturelle pour A = 1 vaut", wn_0[0], "rad/s et pour A =", A_values[-1],":", wn_fin[0], "rad/s")
print("=> wn augmente.\n")
print("Le coefficient d'amortissement pour A = 1 vaut", z_0[0], "et pour A =", A_values[-1],":", z_fin[0])
print("=> z diminue.\n")
# Pôles
# -----
# Création de la fenêtre à une taille donnée
fig = plt.figure("Pole Zero Map",figsize=(20,10))
ax = fig.subplots()
# Pour pouvoir boucler sur les couleurs standards afin de directement jouer avec les couleurs des graphes
from itertools import cycle
prop_cycle = plt.rcParams['axes.prop_cycle']
colors = cycle(prop_cycle.by_key()['color'])
# Trace les poles et zéros pour chacune des fonctions de transfert stockées dans 'g'
for i, H_BF in enumerate(H_BFs):
poles, zeros = rlf.pzmap(H_BF, NameOfFigure="Pole Zero Map", sysName=A_values[i], color=next(colors));
left, right = plt.xlim() # Stocke les limites gauche et droite du graphe
plt.plot([left, right], [0, 0], 'k:'); # Ligne horizontale passant par 0 pour marquer l'axe des imaginaires
poles_0, __ = ml.pzmap(H_BFs[0], plot=False);
poles_fin, __ = ml.pzmap(H_BFs[-1], plot=False);
print("La pseudo pulsation pour A = 1 vaut", poles_0.imag[0], "rad/s et", poles_0.imag[-1], "rad/s et pour A =", A_values[-1],":", poles_fin.imag[0], "rad/s et", poles_fin.imag[-1], "rad/s")
print("=> wd diverge de 0 => Le système oscille plus.\n")
print("L'amortissement pour A = 1 vaut", poles_0.real[0], "et", poles_0.real[-1], "et pour A =", A_values[-1],":", poles_fin.real[0], "et", poles_fin.real[-1])
print("=> sigma converge vers une seule valeur => Le système est plus rapide.\n")
La pulsation naturelle pour A = 1 vaut 7804.962431970385 rad/s et pour A = 100 : 8750.0 rad/s
=> wn augmente.
Le coefficient d'amortissement pour A = 1 vaut 1.0 et pour A = 100 : 0.45693277310924363
=> z diminue.
La pseudo pulsation pour A = 1 vaut 0.0 rad/s et 0.0 rad/s et pour A = 100 : 7783.135775716877 rad/s et -7783.135775716877 rad/s
=> wd diverge de 0 => Le système oscille plus.
L'amortissement pour A = 1 vaut -7804.962431970385 et -191.36109744137914 et pour A = 100 : -3998.161764705882 et -3998.161764705882
=> sigma converge vers une seule valeur => Le système est plus rapide.
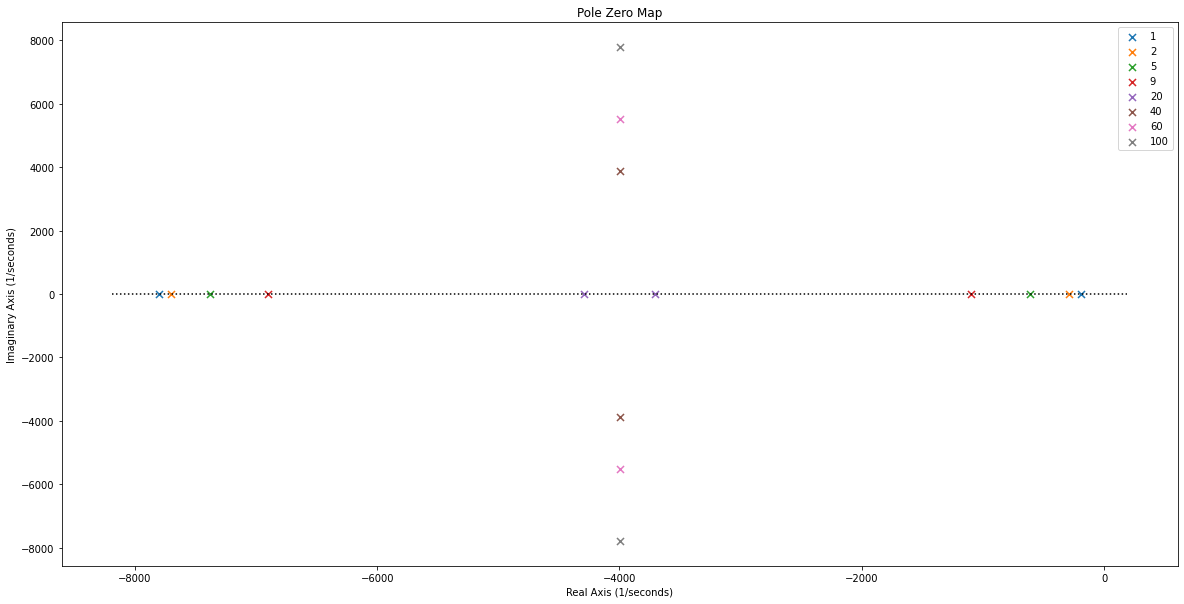
En déduire l’effet d’un correcteur proportionnel sur le régime transitoire: …
Un correcteur proportionnel a pour effet de rendre le système plus rapide (= diminuer le temps de montée) au détriment de la stabilité du système en régime transitoire.
