Contents

Séance 5

Séance 5

Objectifs de la séance

  • Régulateur P

  • Analyse de la stabilité/instabilité

  • Régulateur PI

  • Construction asymptotiques du diagramme de Bode par décomposition de la fonction de transfert en fonctions simples

Régulateur P

Soit la fonction de l’exercice 1 (cf. p. 7-3):

\[ G(p) = \frac{1}{(1+0,5p)*(1+0,25p)} \]

Déterminez, à l’aide du diagramme de Nichols, le correcteur P qui permette de translater la courbe pour une marge de phase de 45° : \(K_P\)= …

Astuce

Une fonction fournie dans le package ReguLabFct permet d’obtenir le gain et la fréquence d’un système donnée à une phase donnée. Il s’agit de la fonction getValues (cf. documentation du package ReguLabFct).

G1 = ml.tf(1, [0.5, 1])
G2 = ml.tf(1, [0.25, 1])
G = G1*G2

fig = plt.figure("Nichols", figsize=(20,10))
rlf.nichols(G, labels=['G(p)'], NameOfFigure = "Nichols")

fig = plt.figure("Bode", figsize=(20,10))
ax = fig.subplots()
mag, w = rlf.getValues(G, -135, printValue=True, NameOfFigure="Bode")

Kp = 1/mag  # Kp va à l'inverse de ce qu'on mesure
print("Kp =", Kp)

Gain à -135° = -17.56544890480597 dB
Fréquence à -135° = 7.1233661553256065 rad/sec
Kp = 7.5556606703682965
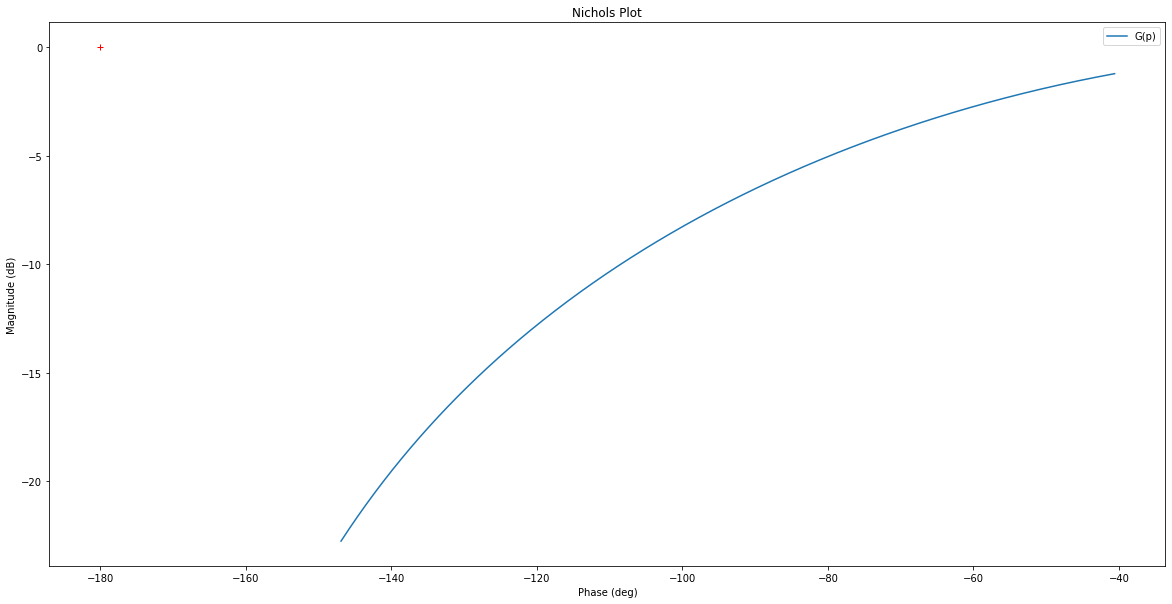
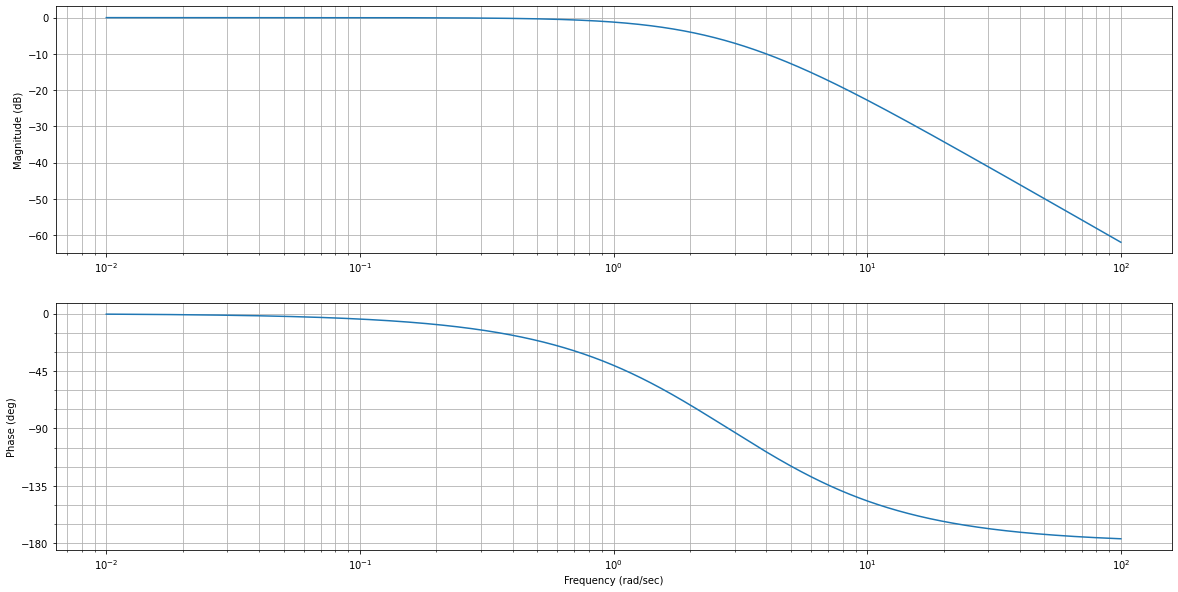
../_images/LaboSeance5_4_1.png ../_images/LaboSeance5_4_2.png

Visualisez l’effet sur la réponse indicielle:

G_BF = ml.feedback(G, 1)
G_BF_Kp = ml.feedback(Kp*G, 1)

fig = plt.figure("Steps", figsize=(20,10))
rlf.stepWithInfo(G_BF, NameOfFigure="Steps")
rlf.stepWithInfo(G_BF_Kp, NameOfFigure="Steps");
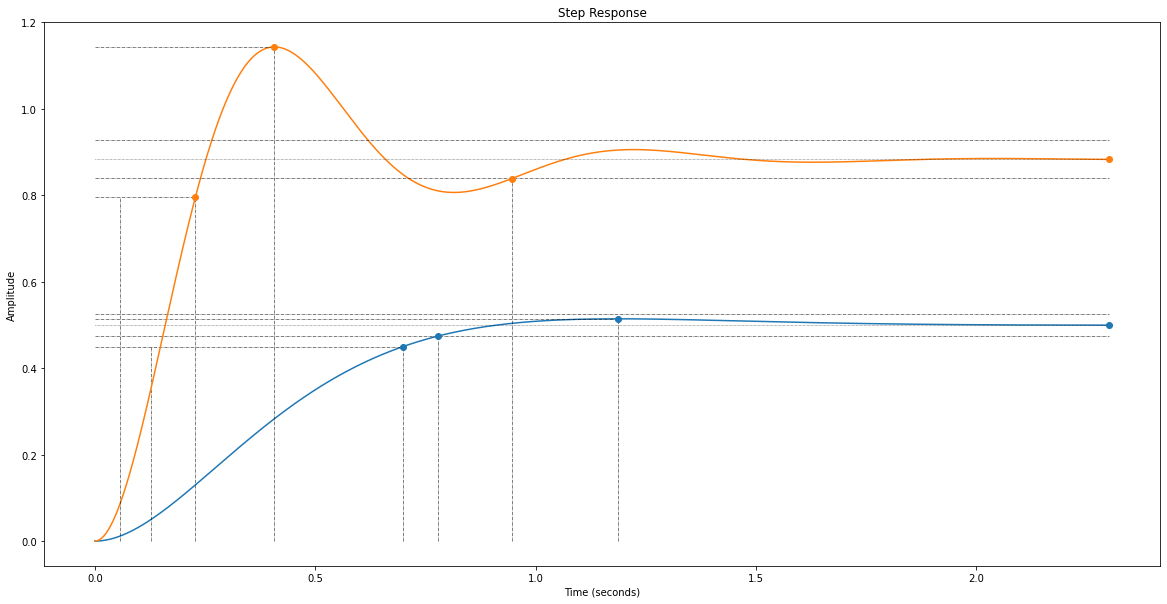
../_images/LaboSeance5_6_0.png

Limite de stabilité

Analysez le système asservi à retour unitaire dont la fonction de transfert de boucle ouverte est la suivante (cf. p 7-11):

\[ G(p) = \frac{1}{(1+0,5p)*(1+4p)*(0.1p+1)} \]

Nichols

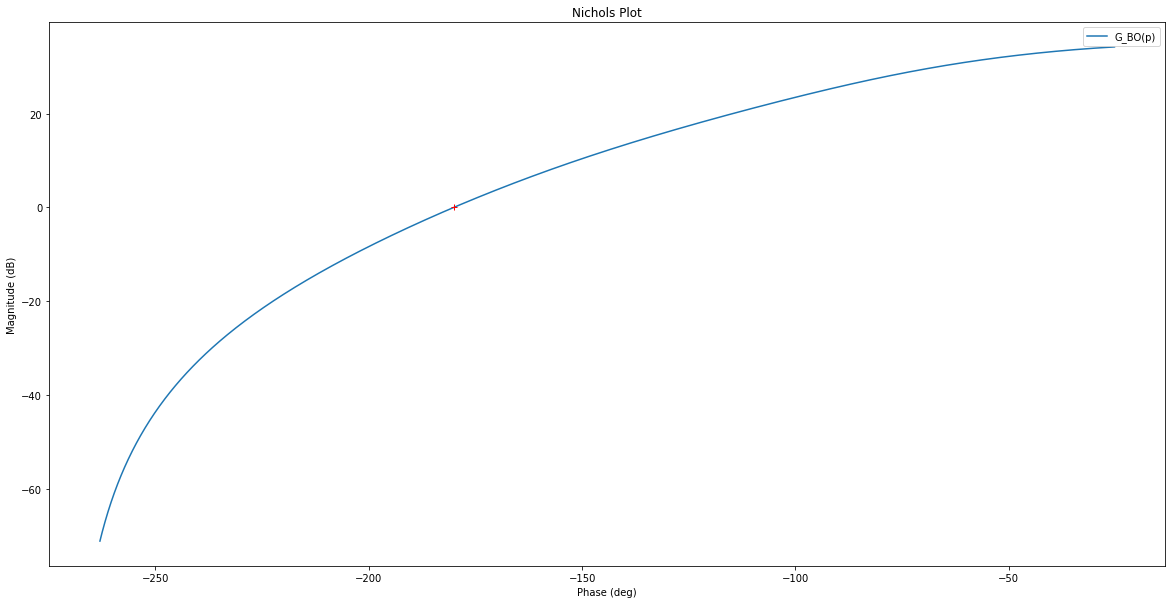
Observez l’allure de \(G_{BO}(p)\) sur le diagramme de Nichols et mesurez la marge de phase et la marge de gain ainsi que des pulsations correspondantes:

  • \(M_\Phi\) = …

  • \(M_G\) = …

Astuce

Pour calculer la marge de gain et de phase d’un système, vous pouvez utiliser la fonction margin du package control.

Exemple:

from control import matlab as ml
G_BO = ml.tf(1, [1, 1])
mg, mp, __, __ = ml.margin(G_BO)

G1 = ml.tf(1, [0.5, 1])
G2 = ml.tf(1, [4, 1])
G3 = ml.tf(1, [0.1, 1])
G_BO = G1*G2*G3

fig = plt.figure("Nichols", figsize=(20,10))
rlf.nichols(G_BO, labels=['G_BO(p)'], NameOfFigure = "Nichols")

mg, mp, __, __ = ml.margin(G_BO)
mg = 20*np.log10(mg)  # Conversion de mg en dB
print("Marge de phase = {MP}° \nMarge de gain = {MG} dB".format(MP=mp, MG=mg))

Marge de phase = inf° 
Marge de gain = 34.86235250429483 dB
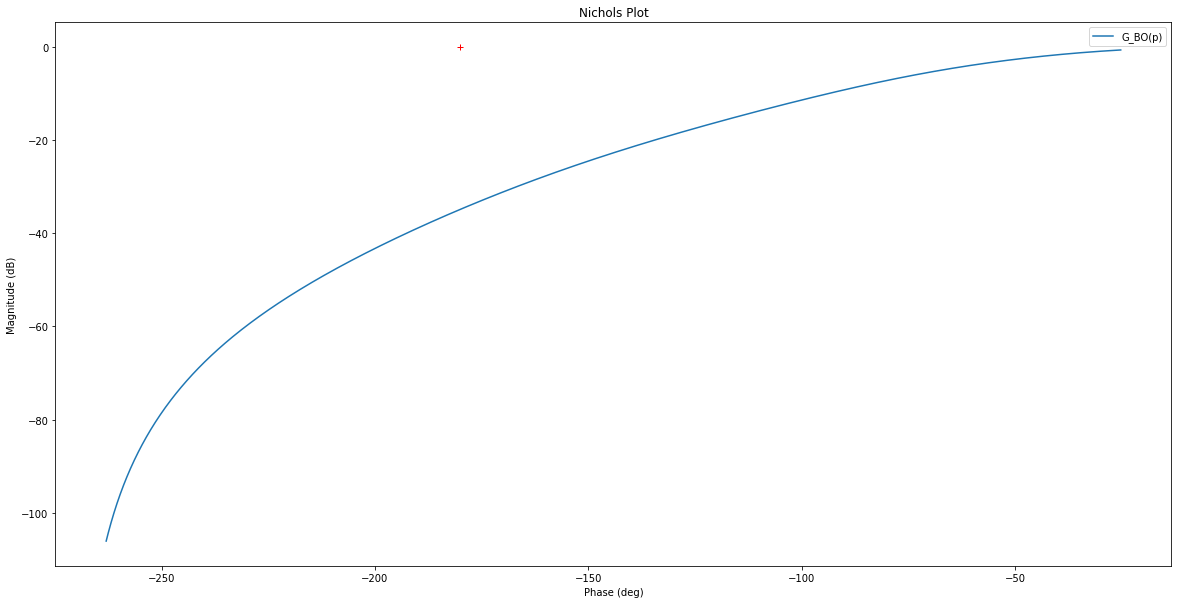
../_images/LaboSeance5_8_1.png

Calculez la valeur critique de \(K_p\) pour passer par le point « -1 » càd (0dB, -180°) : \(K_p\) = …

Kp = 10**(mg/20) # Kp ne doit pas être en dB => conversion
print("Kp =", Kp)

fig = plt.figure("Nichols", figsize=(20,10))
rlf.nichols(Kp*G_BO, labels=['G_BO(p)'], NameOfFigure = "Nichols")

G_BF= ml.feedback(Kp*G_BO)
fig = plt.figure("Steps", figsize=(20,10))
rlf.step_(G_BF, NameOfFigure="Steps");

Kp = 55.349999999999994
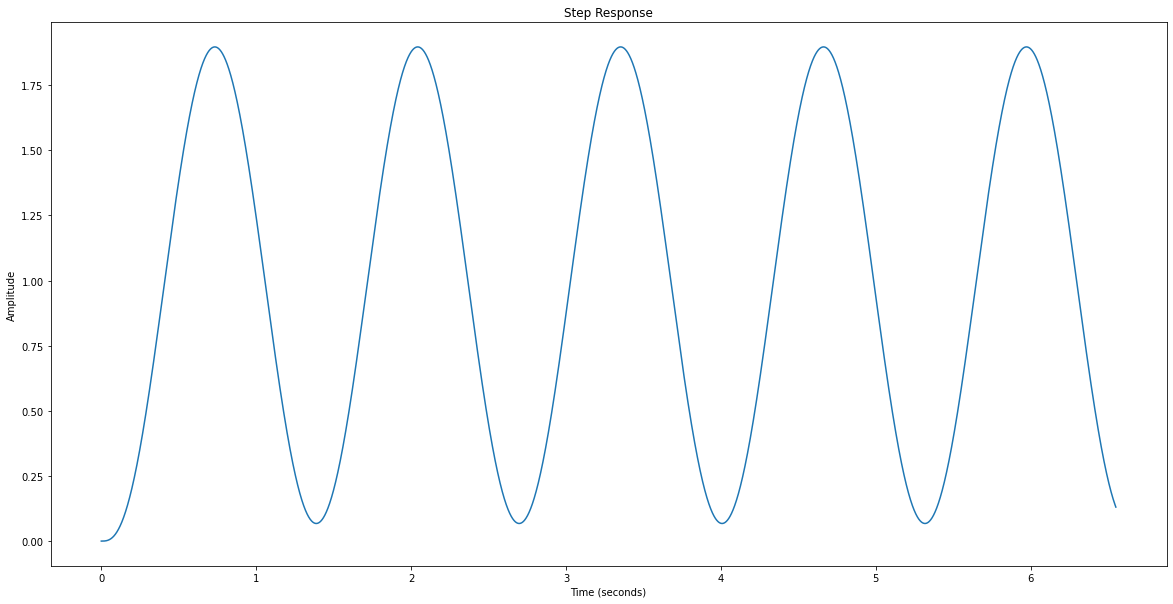
../_images/LaboSeance5_10_1.png ../_images/LaboSeance5_10_2.png

Step

Avec \(K_p = 54\), observez la réponse indicielle.

Kp = 54
G_BF= ml.feedback(Kp*G_BO)
fig = plt.figure("Steps", figsize=(20,10))
rlf.step_(G_BF, NameOfFigure="Steps");
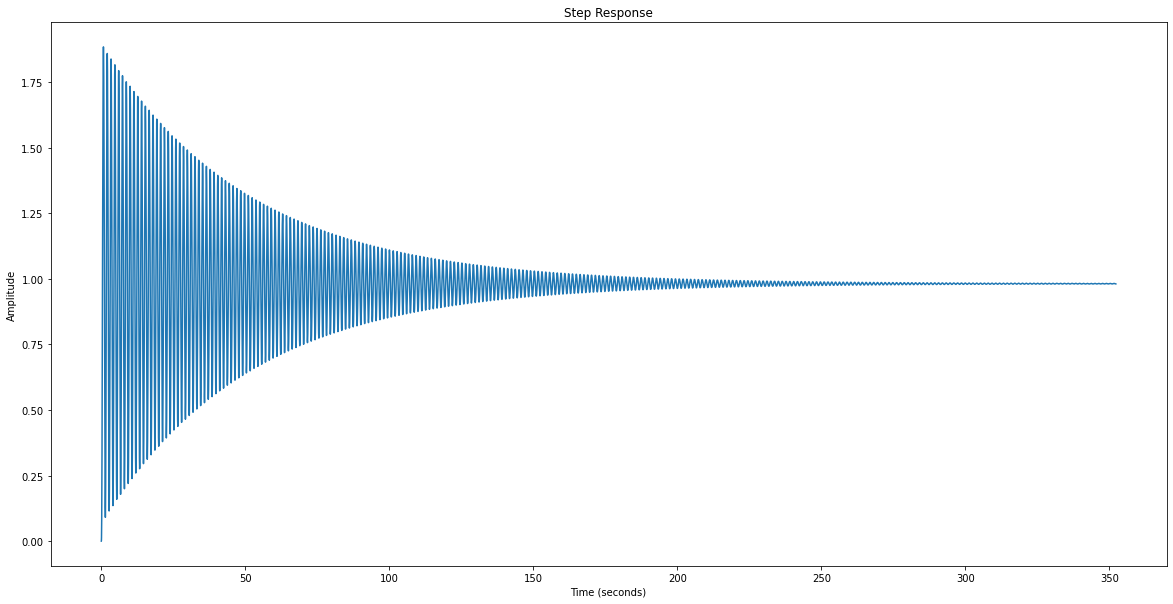
../_images/LaboSeance5_12_0.png

Que se passe-t-il si on insère un correcteur proportionnel de gain \(K_p = 56\) ?

Kp = 56
G_BF= ml.feedback(Kp*G_BO)
fig = plt.figure("Steps", figsize=(20,10))
rlf.step_(G_BF, NameOfFigure="Steps");
../_images/LaboSeance5_14_0.png

Calculez \(K_p\) pour obtenir une marge de phase de 45° :

Astuce

Pour calculer la valeur du gain et/ou de la fréquence d’un système à une marge de phase donnée, vous pouvez utiliser la fonction getValues du package ReguLabFct.

mag, w = rlf.getValues(G_BO, -135, NameOfFigure="Bode Gbo") # -135° car on souhaite regarder le gain du système en BO à 45° du point critique (-180°, 0dB)
Kp_45 = 1/mag  # Donne directement la valeur de l'amplitude => Pas besoin de la convertir à partir d'une valeur en dB + Kp va à l'inverse de ce qu'on mesure
print("Kp =", Kp_45)

fig = plt.figure("Nichols", figsize=(20,10))
rlf.nichols(Kp_45*G_BO, labels=['Kp_45*G_BO(p)'], NameOfFigure = "Nichols")
__, mp, __, __ = ml.margin(Kp_45*G_BO)
print("Marge de phase = {MP}°".format(MP=mp))

Gain à -135° = -20.136844108498554 dB
Fréquence à -135° = 1.8273687032470145 rad/sec
Kp = 10.158795207791778
Marge de phase = 45.016953712610785°
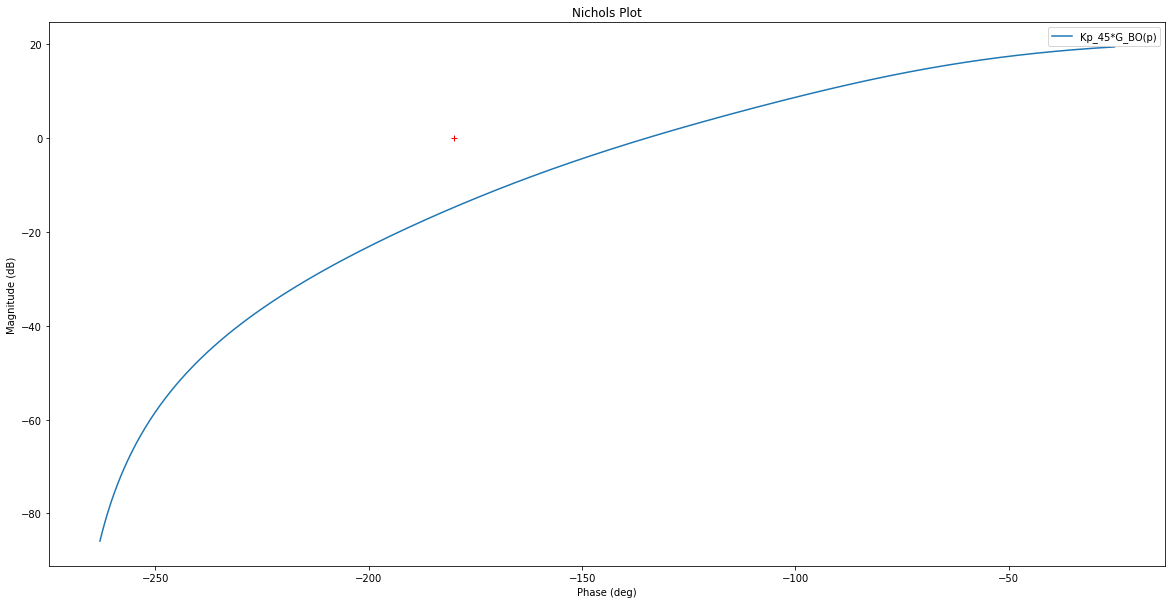
../_images/LaboSeance5_16_1.png ../_images/LaboSeance5_16_2.png

Calculez \(K_p\) pour obtenir une marge de phase de 60° :

mag, w = rlf.getValues(G_BO, -120, NameOfFigure="Bode Gbo") # -120° car on souhaite regarder le gain du système en BO à 60° du point critique (-180°, 0dB)
Kp_60 = 1/mag  # Donne directement la valeur de l'amplitude => Pas besoin de la convertir à partir d'une valeur en dB + Kp va à l'inverse de ce qu'on mesure
print("Kp =", Kp_60)

fig = plt.figure("Nichols", figsize=(20,10))
rlf.nichols(Kp*G_BO, labels=['Kp_60*G_BO(p)'], NameOfFigure = "Nichols")
__, mp, __, __ = ml.margin(Kp_60*G_BO)
print("Marge de phase = {MP}°".format(MP=mp))

Gain à -120° = -16.200670408217633 dB
Fréquence à -120° = 1.3140499110790103 rad/sec
Kp = 6.457040648746092
Marge de phase = 59.97990291672397°
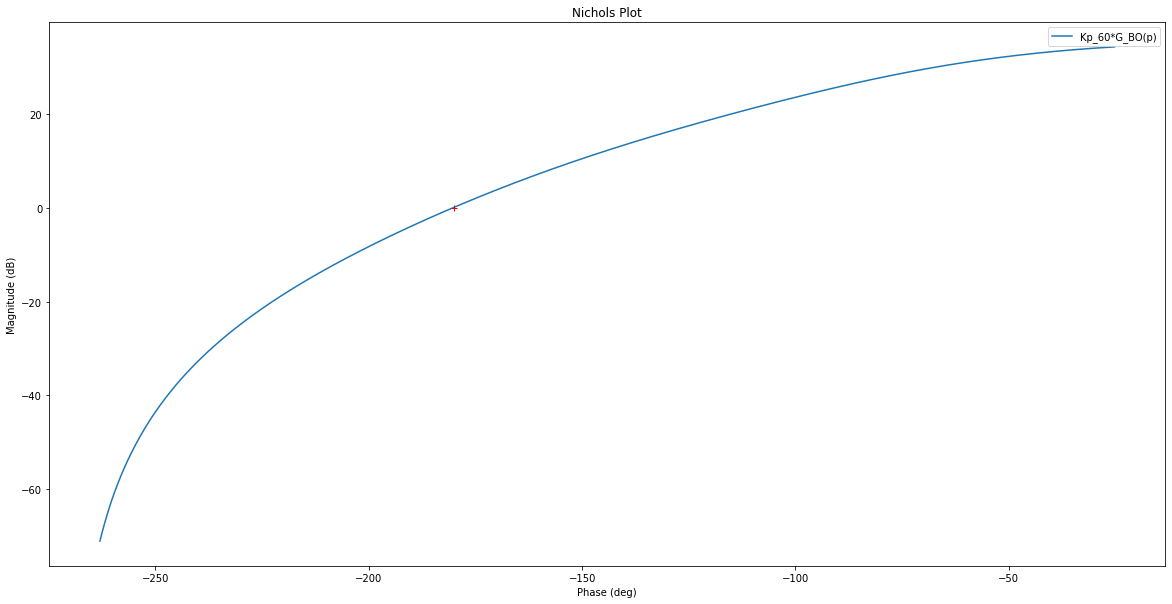
../_images/LaboSeance5_18_1.png ../_images/LaboSeance5_18_2.png

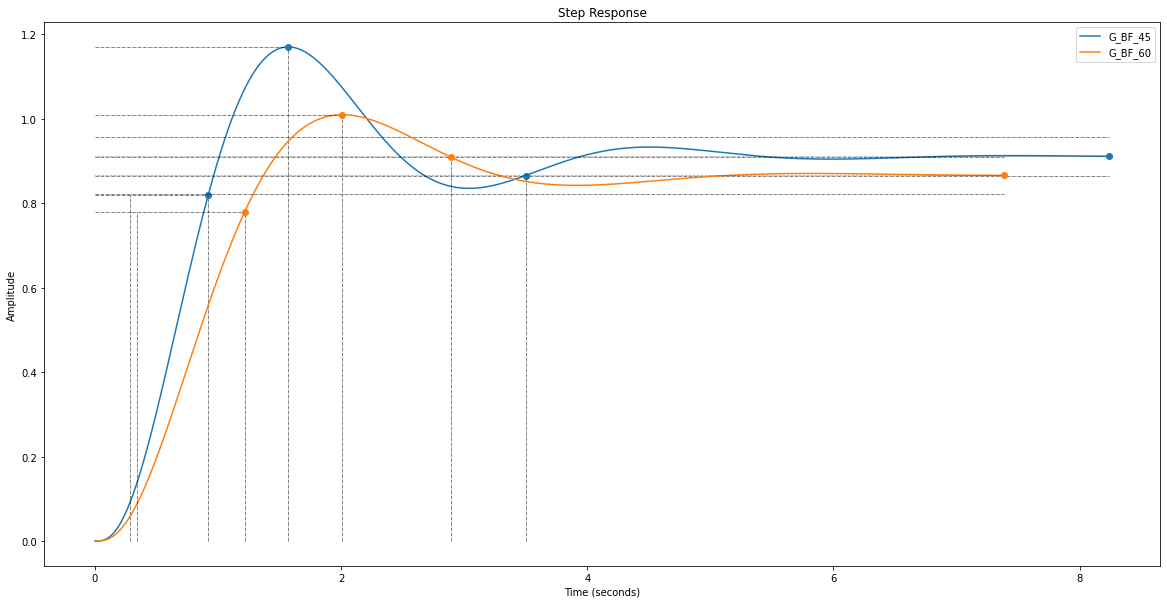
Et comparez les réponses indicielles respectives pour ces 2 marges typiques habituelles.

G_BF_45= ml.feedback(Kp_45*G_BO)
G_BF_60= ml.feedback(Kp_60*G_BO)
fig = plt.figure("Steps", figsize=(20,10))
rlf.stepWithInfo(G_BF_45, NameOfFigure="Steps", sysName='G_BF_45')
rlf.stepWithInfo(G_BF_60, NameOfFigure="Steps", sysName='G_BF_60');
../_images/LaboSeance5_20_0.png

[Facultatif] Faites l’exercice 2 page 7-4 et visualisez les calculs par une résolution graphique

[Facultatif] Faites aussi l’exercice 3.

[Facultatif] application 1 : régulation de vitesse

Tracez le diagramme de Nichols qui permette de déterminer graphiquement la valeur max de A pour minimiser l’erreur tout en garantissant une marge de phase de 45° ou de 60° et comparez avec la solution A=100.

[Facultatif] Régulation de position

Tracez le diagramme de Nichols qui permette de déterminer graphiquement la valeur max de A pour minimiser l’erreur tout en garantissant une marge de phase de 45°.

Comparez à la résolution temporelle …

Pour rappel, vous pouvez facilement obtenir les valeurs typiques d’une fonction d’ordre 2 grâce à la fonction damp du package control.

Régulateur PI

Système du \(3^e\) ordre

Soit le système asservi à retour unitaire dont la fonction de boucle ouverte est :

\[ G(p)=\frac{7500}{(p+4)(p+10)(p+500)} \]

Ramenez le système à ses 2 pôles dominants.

Si on écrit G(p) sous sa forme canonique, on a:

\[ G(p)=\frac{\frac{1}{4}*\frac{1}{10}*\frac{1}{500}*7500}{(\frac{1}{4}p+1)(\frac{1}{10}p+1)(\frac{1}{500}p+1)} \]

\(\Rightarrow\) Le pôle le moins dominant est celui dont la constante de temps est la plus faible, soit \(\frac{1}{500}\). Dès lors, si on approxime G(p) à un système d’ordre 2 en retirant son pôle le moins dominant, on obtient:

\[ G_{approx}(p)=\frac{0.375}{(\frac{1}{4}p+1)(\frac{1}{10}p+1)} \]

Vérifiez dans Nichols et sur la réponse indicielle.

G1 = ml.tf(7500/4/10/500, [1/4, 1])
G2 = ml.tf(1, [1/10, 1])
G3 = ml.tf(1, [1/500, 1])
G = G1*G2*G3
G_approx = G1*G2

# Nichols
fig = plt.figure("Nichols", figsize=(20,10))
frequencies = np.linspace(10**-5, 10**5, 10**6) # Pour bien voir vers où on converge dans les hautes fréquences (jusqu'à 10^5 rad/s ici)
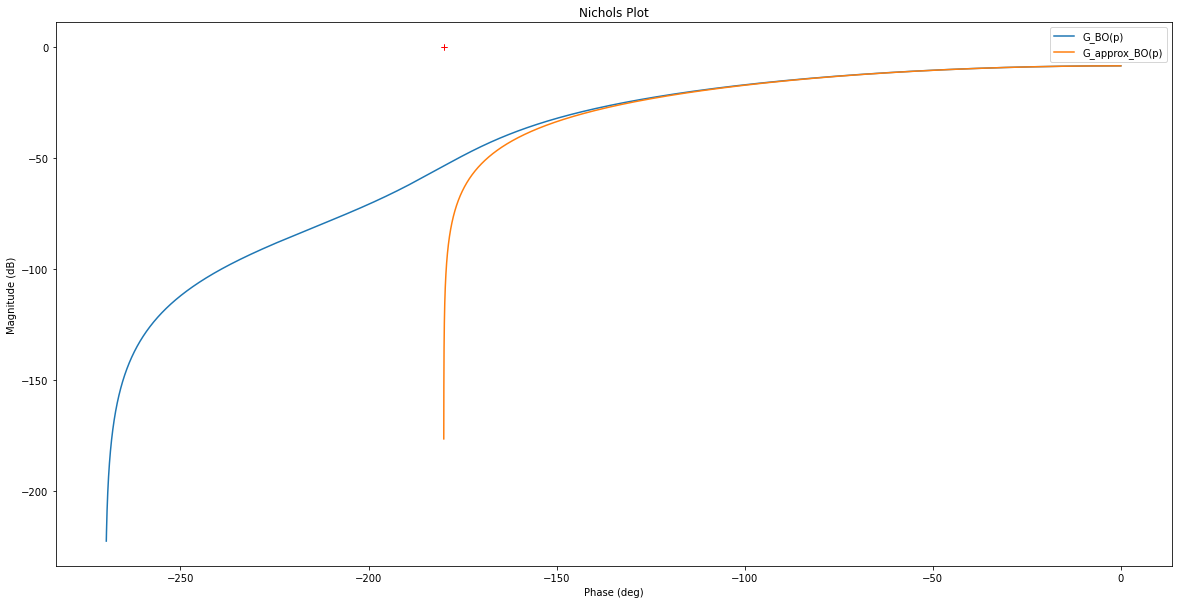
rlf.nichols(G, labels=['G_BO(p)'], NameOfFigure = "Nichols", omega=frequencies)
rlf.nichols(G_approx, labels=['G_approx_BO(p)'], NameOfFigure = "Nichols", omega=frequencies)

# Réponse indicielle
G_BF = ml.feedback(G, 1)
G_approx_BF = ml.feedback(G_approx, 1)

fig = plt.figure("Steps", figsize=(20,10))
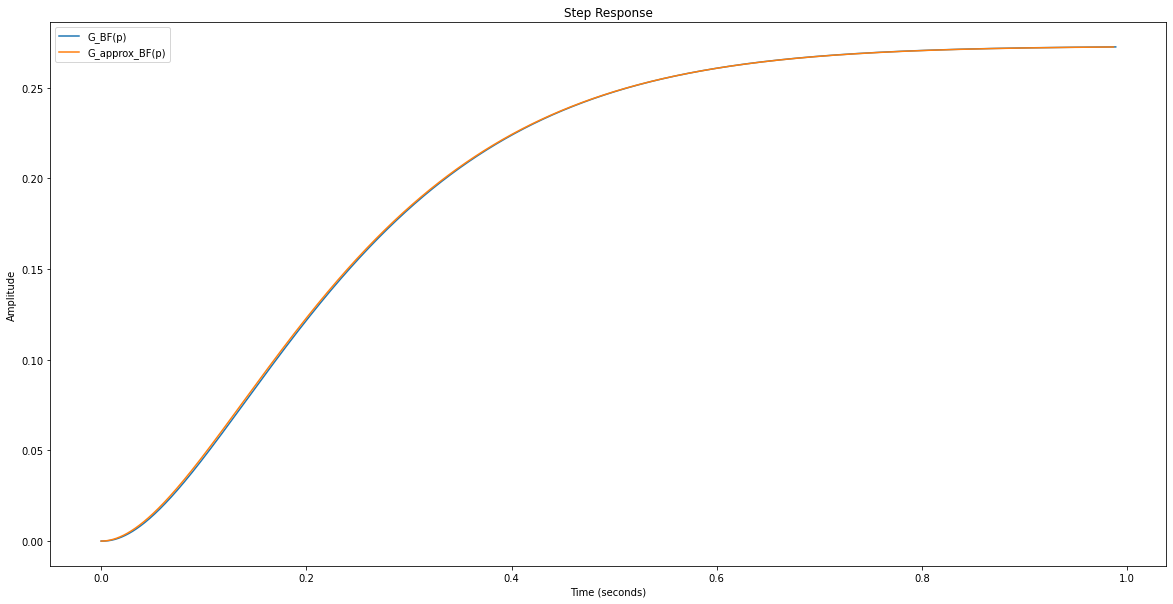
rlf.step_(G_BF, NameOfFigure="Steps", sysName='G_BF(p)')
rlf.step_(G_approx_BF, NameOfFigure="Steps", sysName='G_approx_BF(p)');
../_images/LaboSeance5_27_0.png ../_images/LaboSeance5_27_1.png

On demande de déterminer le correcteur PI dont le but est d’annuler l’erreur en régime permanent tout en assurant une réponse indicielle dont le dépassement est limité à 10% (tablez ici sur une marge de phase de 60°).

  • Par la méthode du pôle dominant

  • Par la méthode de placement fréquentiel

Tracez le diagramme de Nichols ainsi corrigé pour le système réel et pour le système ramené à 2 pôles dominants.

Tracez également les 2 réponses indicielles.

Méthode de compensation du pôle dominant (cf. p. 7-8)

Il faut tout d’abord lire la valeur du gain lorsqu’on est à 60° de marge de phase (= gain à 60° du point d’instabilitité (0, -180°)). Cela peut se faire grâce à la fonction getValues du package ReguLabFct.

# Lecture phase
fig = plt.figure("Bode G_BO", figsize=(20,10))
print("Valeurs pour G_BO:")
mag, w = rlf.getValues(G, -180+60, NameOfFigure="Bode G_BO")

Valeurs pour G_BO:

Gain à -120° = -21.547793018711413 dB
Fréquence à -120° = 11.228067905278133 rad/sec
../_images/LaboSeance5_30_2.png

On peut ensuite en déterminer \(K_P\) en faisant bien attention que le gain mesuré est en dB et qu’il faut s’y opposer pour atteindre une valeur de 0 dB.

\[\Rightarrow 20*\log(K_P) = 21.55\]

Pour trouver \(\tau_I\), on sait que notre pôle dominant est égale à -4. Dès lors, on fixe \(\tau_I=\frac{1}{4}\) secondes.

Maintenant que nous connaissons les paramètres \(K_P\) et \(\tau_I\) de notre correcteur PI, il ne reste plus qu’à implémenter ce dernier! Ceci se fait ainsi en code python:

Kp = 10**(21.55/20)

tI = 1/4
C_I = ml.tf([tI, 1],[tI, 0])

G_BO_PI = Kp*C_I*G
G_approx_BO_PI = Kp*C_I*G_approx

# Nichols
fig = plt.figure("Nichols - Pôles dominants", figsize=(20,10))
frequencies = np.linspace(10**-5, 10**5, 10**6) # Pour bien voir vers où on converge dans les hautes fréquences (jusqu'à 10^5 rad/s ici)
rlf.nichols(Kp*G, labels=['G_BO_Kp(p)'], NameOfFigure = "Nichols - Pôles dominants", omega=frequencies)
rlf.nichols(G_BO_PI, labels=['G_BO_PI(p)'], NameOfFigure = "Nichols - Pôles dominants", omega=frequencies)
rlf.nichols(G_approx_BO_PI, labels=['G_approx_BO_PI(p)'], NameOfFigure = "Nichols - Pôles dominants", omega=frequencies)

# Réponse indicielle
G_BF_Kp = ml.feedback(Kp*G, 1)
G_BF_PI = ml.feedback(G_BO_PI, 1)
G_approx_BF_PI = ml.feedback(G_approx_BO_PI, 1)

fig = plt.figure("Steps - Pôles dominants", figsize=(20,10))
info = rlf.stepWithInfo(G_BF_Kp, NameOfFigure="Steps - Pôles dominants", sysName='G_BF_Kp(p)')
info = rlf.stepWithInfo(G_BF_PI, NameOfFigure="Steps - Pôles dominants", sysName='G_BF_PI(p)')
info_approx = rlf.stepWithInfo(G_approx_BF_PI, NameOfFigure="Steps - Pôles dominants", sysName='G_approx_BF_PI(p)');

# Pour vérifier que la marge de phase est bonne
mg, mp, __, __ = ml.margin(Kp*G)
print("Marge de phase système original corrigé par Kp =", mp, "°")
mg, mp, __, __ = ml.margin(G_BO_PI)
print("Marge de phase système original corrigé par PI =", mp, "°")
mg, mp, __, __ = ml.margin(G_approx_BO_PI)
print("Marge de phase système approx corrigé par PI =", mp, "°\n")

# Dépassement
print("Dépassement système original corrigé par PI =", info.Overshoot, "%")
print("Dépassement système approx corrigé par PI =", info_approx.Overshoot, "%")

Marge de phase système original corrigé par Kp = 60.00267242116146 °
Marge de phase système original corrigé par PI = 39.26601808288615 °
Marge de phase système approx corrigé par PI = 40.59772796407222 °

Dépassement système original corrigé par PI = 29.787597954275036 %
Dépassement système approx corrigé par PI = 28.222220587721438 %
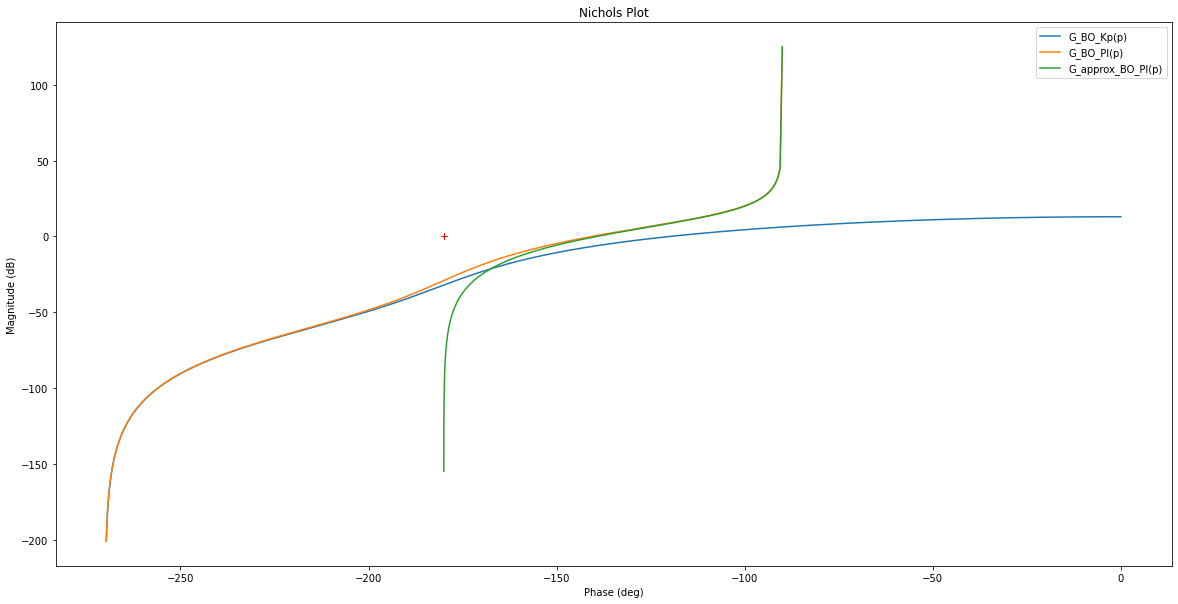
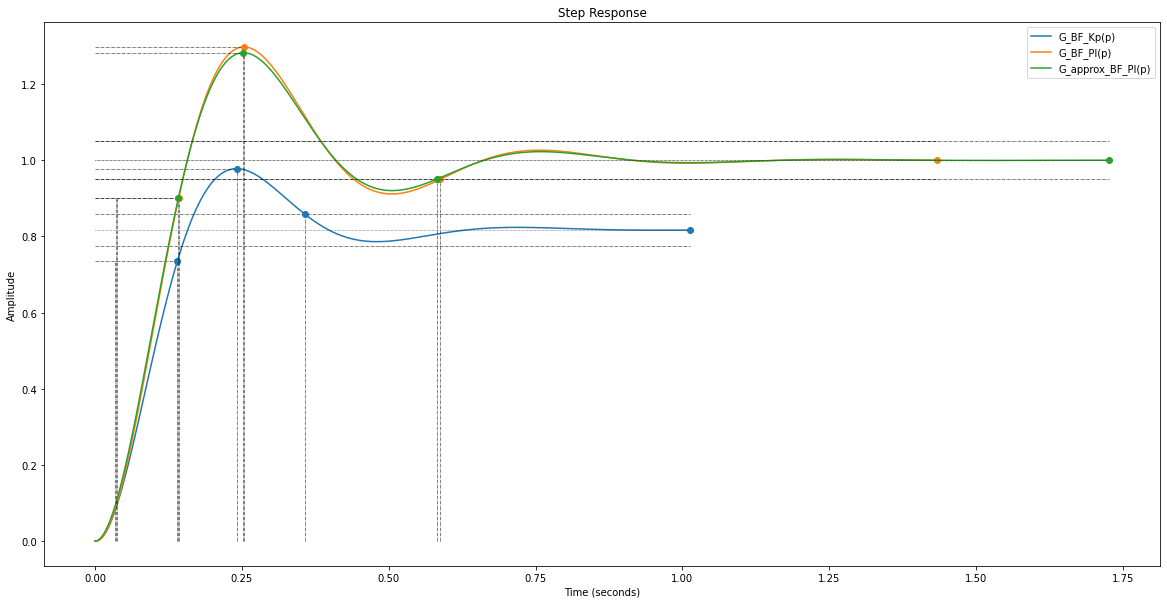
../_images/LaboSeance5_32_1.png ../_images/LaboSeance5_32_2.png

On remarque que bien que le \(K_P\) ait corrigé correctement le système donné (on a bien 60° de marge de phase), ceci n’est plus la cas lorsqu’on ajoute le correcteur I (on obtient un marge de phase d’environ 40°)… Il faut donc réitérer l’opération en rajoutant un \(K_P\) supplémentaire afin de descendre la courbe de Nichols du système et ainsi garantir une marge de phase de 60°.

# Lecture phase
fig = plt.figure("Bode G_BO_PI", figsize=(20,10))
print("Valeurs pour G_BO_PI:")
mag, w = rlf.getValues(G_BO_PI, -180+60, NameOfFigure="Bode G_BO_PI")

Valeurs pour G_BO_PI:
Gain à -120° = 8.871141985102017 dB
Fréquence à -120° = 5.626975542423636 rad/sec
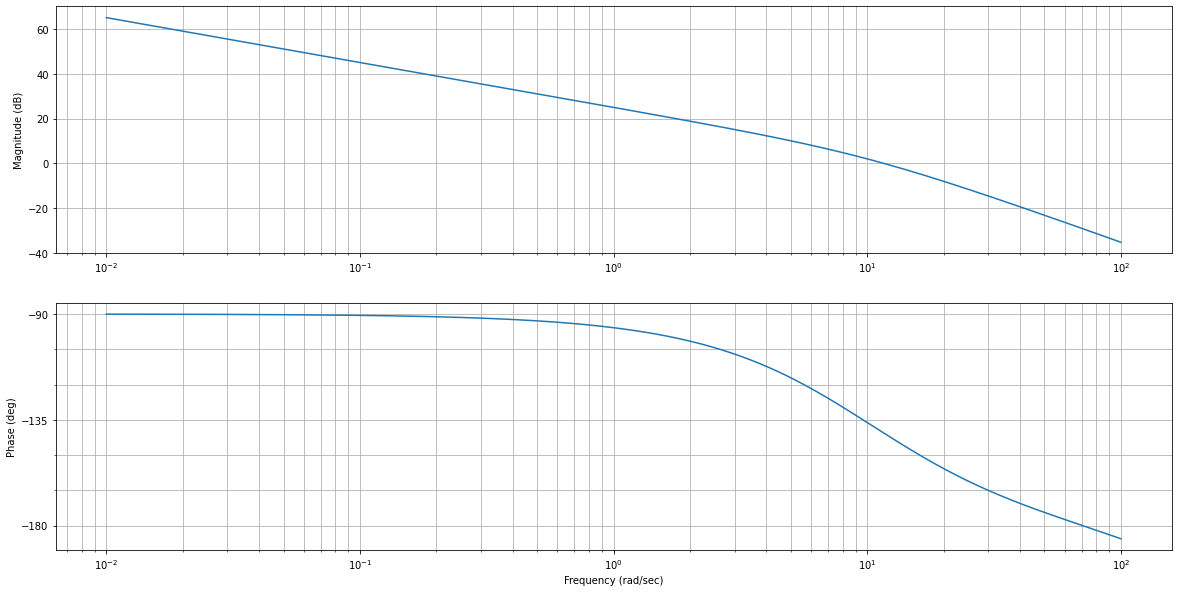
../_images/LaboSeance5_34_1.png

On peut ensuite en déterminer \(K_{P_2}\) en faisant bien attention que le gain mesuré est en dB et qu’il faut s’y opposer pour atteindre une valeur de 0dB.

\[\Rightarrow 20*\log(K_{P_2}) = -8.87\]

En utilisant ce nouveau \(K_P\), on otbient:

Kp_1 = Kp
Kp_2 = 10**(-8.87/20)
Kp = Kp_1*Kp_2

tI = 1/4
C_I = ml.tf([tI, 1],[tI, 0])

G_BO_PI = Kp*C_I*G
G_approx_BO_PI = Kp*C_I*G_approx

# Nichols
fig = plt.figure("Nichols - Pôles dominants", figsize=(20,10))
frequencies = np.linspace(10**-5, 10**5, 10**6) # Pour bien voir vers où on converge dans les hautes fréquences (jusqu'à 10^5 rad/s ici)
rlf.nichols(G_BO_PI, labels=['G_BO_PI(p)'], NameOfFigure = "Nichols - Pôles dominants", omega=frequencies)
rlf.nichols(G_approx_BO_PI, labels=['G_approx_BO_PI(p)'], NameOfFigure = "Nichols - Pôles dominants", omega=frequencies)

# Réponse indicielle
G_BF_PI = ml.feedback(G_BO_PI, 1)
G_approx_BF_PI = ml.feedback(G_approx_BO_PI, 1)

fig = plt.figure("Steps - Pôles dominants", figsize=(20,10))
info = rlf.stepWithInfo(G_BF_PI, NameOfFigure="Steps - Pôles dominants", sysName='G_BF_PI(p)')
info_approx = rlf.stepWithInfo(G_approx_BF_PI, NameOfFigure="Steps - Pôles dominants", sysName='G_approx_BF_PI(p)');

# Pour vérifier que la marge de phase est bonne
mg, mp, __, __ = ml.margin(G_BO_PI)
print("Marge de phase système original corrigé par PI =", mp, "°")
mg, mp, __, __ = ml.margin(G_approx_BO_PI)
print("Marge de phase système approx corrigé par PI =", mp, "°\n")

# Dépassement
print("Dépassement système original corrigé par PI =", info.Overshoot, "%")
print("Dépassement système approx corrigé par PI =", info_approx.Overshoot, "%")

Marge de phase système original corrigé par PI = 59.98620867072424 °
Marge de phase système approx corrigé par PI = 60.62980341859125 °

Dépassement système original corrigé par PI = 8.629575441367464 %
Dépassement système approx corrigé par PI = 8.21695174459216 %
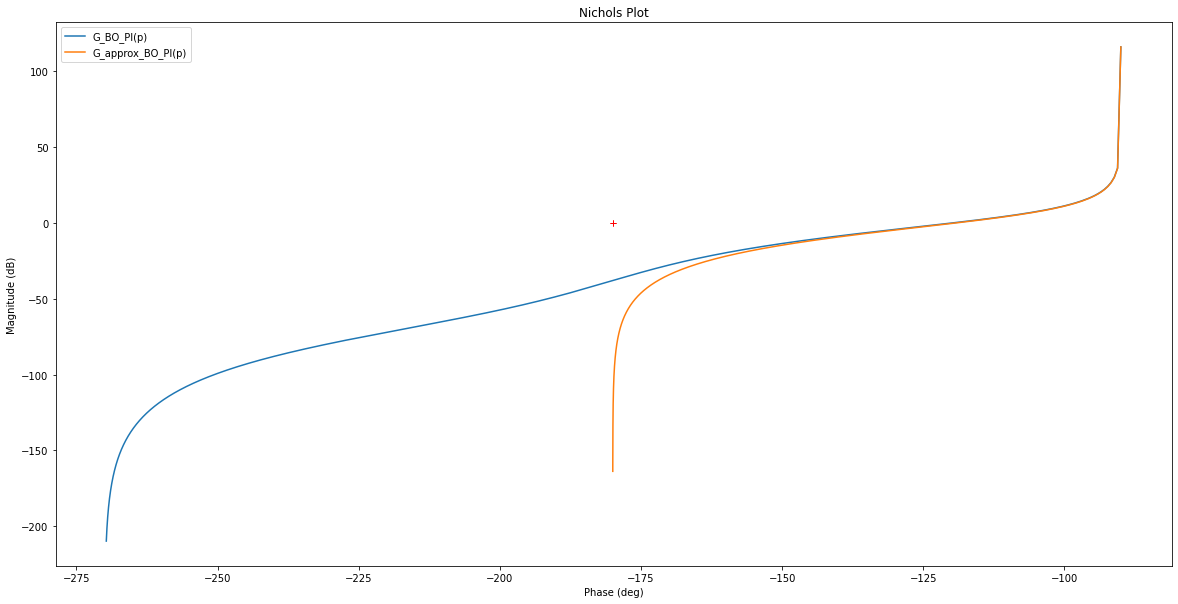
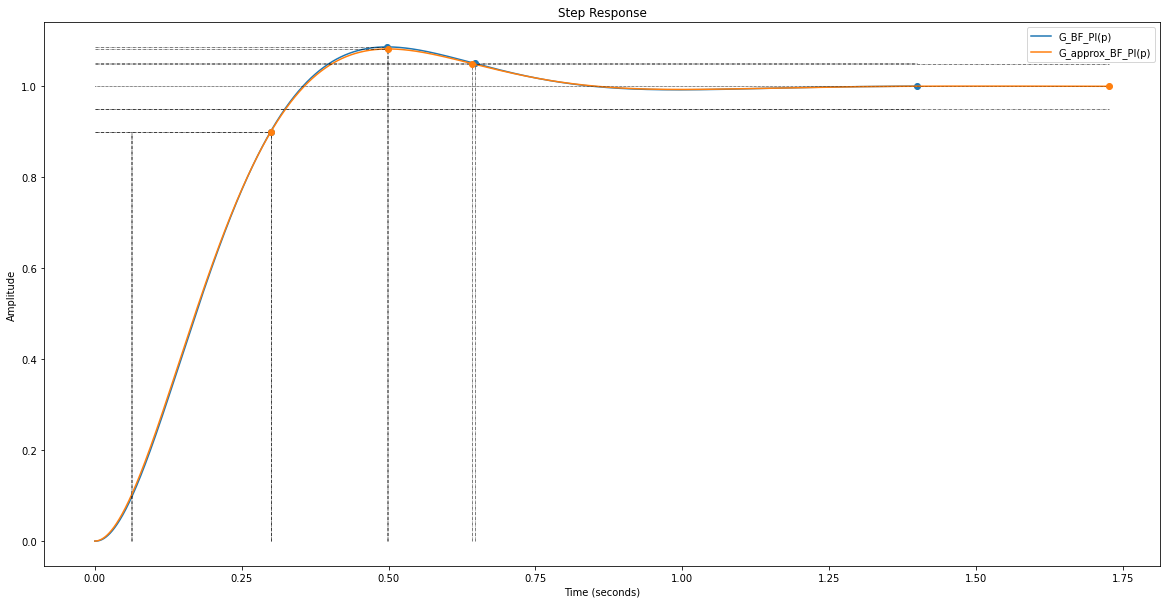
../_images/LaboSeance5_36_1.png ../_images/LaboSeance5_36_2.png

La marge de phase conseillée ici (60°) est maintenant bonne et on observe bien un dépassement inférieur à 10 %.

Méthode de placement fréquentiel (cf. p. 7-8)

La méthode du placement fréquentiel consiste à trouver la pulsation critique (= pulsation à laquelle le gain vaut 0 dB) et de choisir un \(\tau_I>\frac{10}{\omega_{critique}}\) afin que le correcteur PI n’agisse qu’en-deçà de cette pulsation critique.

Comme pour la méthode de compensation du pôle dominant, la première chose à faire est de trouver le \(K_P\) permettant d’assurer la marge de phase souhaitée.

Kp = Kp_1 # On reprend le même Kp que lors de la première étape lors de la technique du pôle dominant puisqu'on souhaite obtenir la même marge de phase (60°).

# Lecture de la fréquence à la phase souhaitée
fig = plt.figure("Bode G_BO", figsize=(20,10))
print("Valeurs pour Kp*G:")
mag, w = rlf.getValues(Kp*G, -180+60, NameOfFigure="Bode G_BO")

Valeurs pour Kp*G:
Gain à -120° = 0.0022069812885906273 dB
Fréquence à -120° = 11.228067905278133 rad/sec
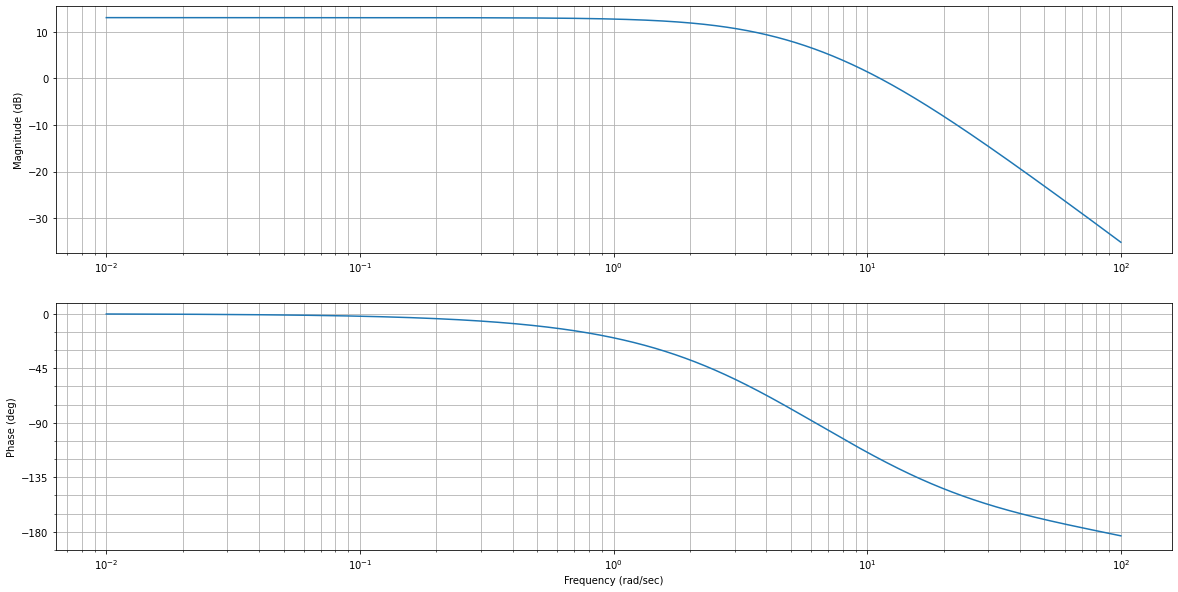
../_images/LaboSeance5_39_1.png

On remarque que la fréqence du système à -120° reste la même que pour le système non corrigé (cf. début de la méthode de la compensation du pôle dominant). Le \(K_P\) n’a donc pas d’effet sur la fréquence du système. On prend donc \(\omega_{critique} = 11.23\) rad/s.

Puisqu’on ne veut pas que le correcteur I agisse au-delà de cette pulsation critique, on fixe \(\tau_I=\frac{10}{\omega_{critique}}\).

w_crit = 11.23
tI = 10/w_crit
C_I = ml.tf([tI, 1],[tI, 0])

G_BO_PI = Kp*C_I*G
G_approx_BO_PI = Kp*C_I*G_approx

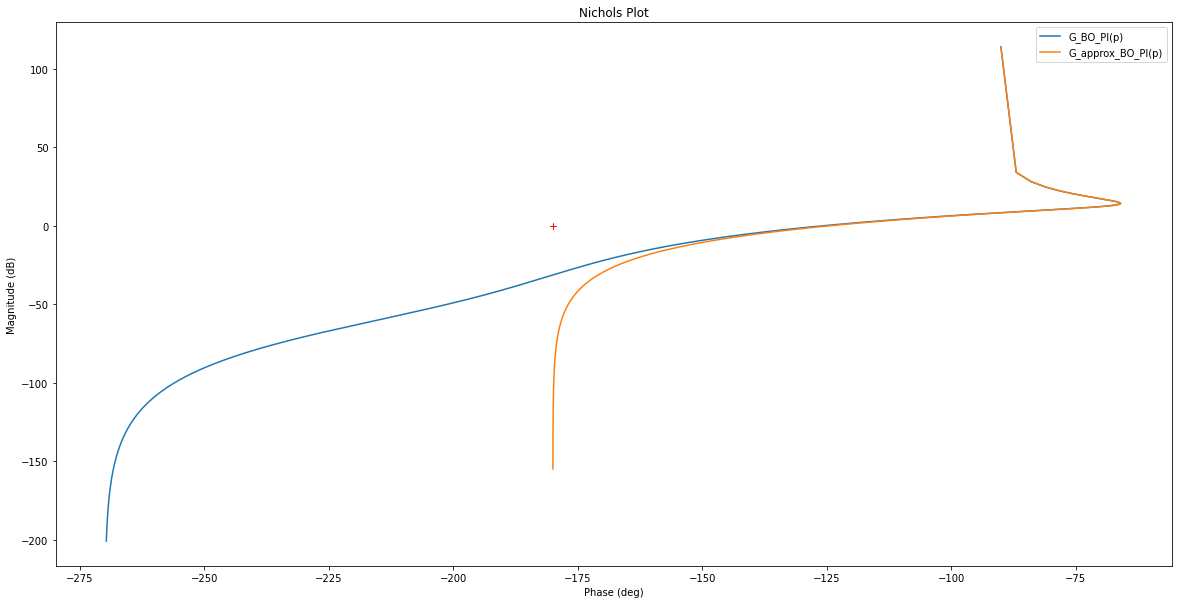
# Nichols
fig = plt.figure("Nichols - Placement fréquentiel", figsize=(20,10))
frequencies = np.linspace(10**-5, 10**5, 10**6) # Pour bien voir vers où on converge dans les hautes fréquences (jusqu'à 10^5 rad/s ici)
rlf.nichols(G_BO_PI, labels=['G_BO_PI(p)'], NameOfFigure = "Nichols - Placement fréquentiel", omega=frequencies)
rlf.nichols(G_approx_BO_PI, labels=['G_approx_BO_PI(p)'], NameOfFigure = "Nichols - Placement fréquentiel", omega=frequencies)

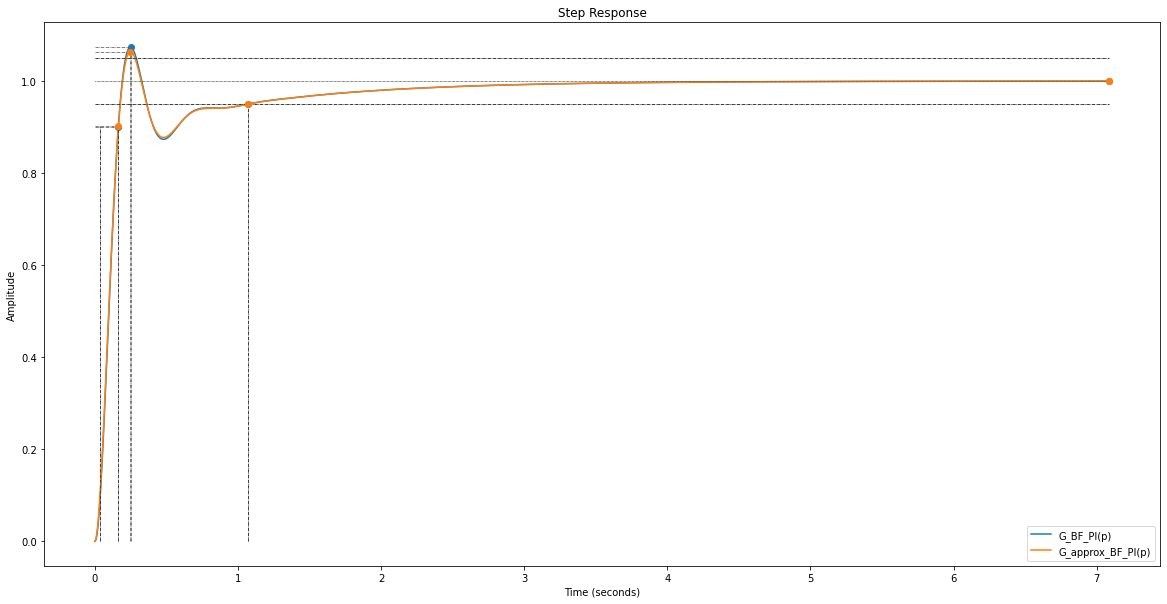
# Réponse indicielle
G_BF_PI = ml.feedback(G_BO_PI, 1)
G_approx_BF_PI = ml.feedback(G_approx_BO_PI, 1)

fig = plt.figure("Steps - Placement fréquentiel", figsize=(20,10))
info = rlf.stepWithInfo(G_BF_PI, NameOfFigure="Steps - Placement fréquentiel", sysName='G_BF_PI(p)')
info_approx = rlf.stepWithInfo(G_approx_BF_PI, NameOfFigure="Steps - Placement fréquentiel", sysName='G_approx_BF_PI(p)');

# Pour vérifier que la marge de phase est bonne
mg, mp, __, __ = ml.margin(G_BO_PI)
print("Marge de phase système original corrigé par PI =", mp, "°")
mg, mp, __, __ = ml.margin(G_approx_BO_PI)
print("Marge de phase système approx corrigé par PI =", mp, "°\n")

# Dépassement
print("Dépassement système original corrigé par PI =", info.Overshoot, "%")
print("Dépassement système approx corrigé par PI =", info_approx.Overshoot, "%")

Marge de phase système original corrigé par PI = 54.14810405581133 °
Marge de phase système approx corrigé par PI = 55.43203927473394 °

Dépassement système original corrigé par PI = 7.4363350761182945 %
Dépassement système approx corrigé par PI = 6.423418111862422 %
../_images/LaboSeance5_41_1.png ../_images/LaboSeance5_41_2.png

Note

On remarque qu’on peut se permettre d’avoir une marge de phase plus petite puisque le dépassement mesuré est assez faible par rapport aux 10% tolérés. On peut donc diminuer \(\tau_I\) en augmentant \(\omega_{critique}\) par essais-erreurs. On obtient par exemple le résultat qui suit pour une \(\omega_{critique}\) de 14$ rad/s.

Marge de phase système original corrigé par PI = 52.681463005553184 °
Marge de phase système approx corrigé par PI = 53.96804155763061 °

Dépassement système original corrigé par PI = 9.751797844378963 %
Dépassement système approx corrigé par PI = 8.69700871832626 %
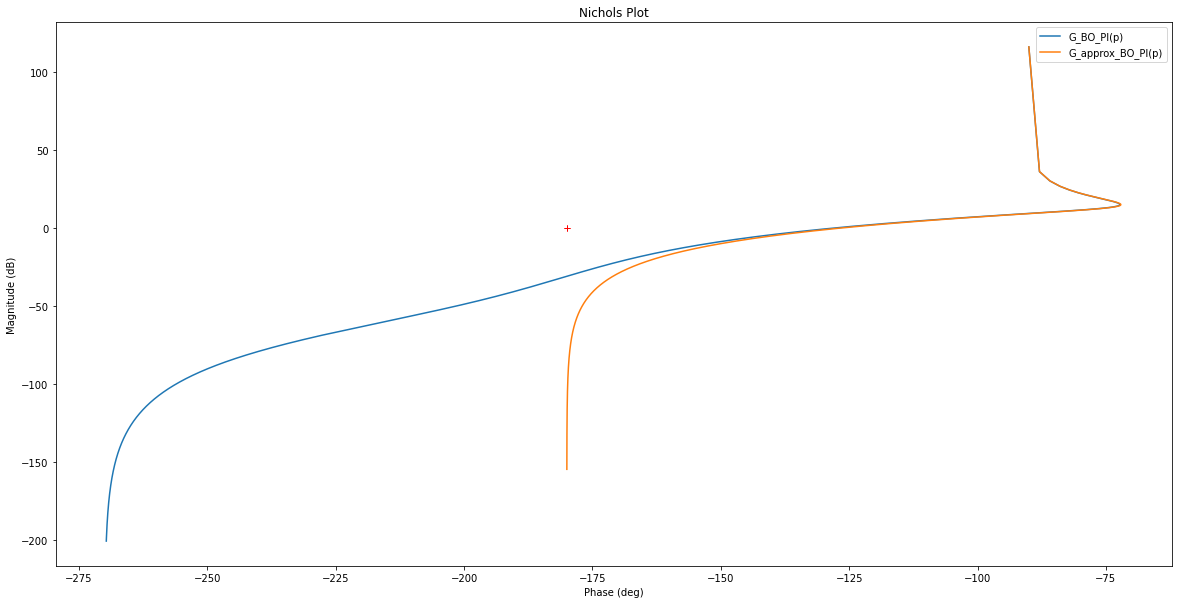
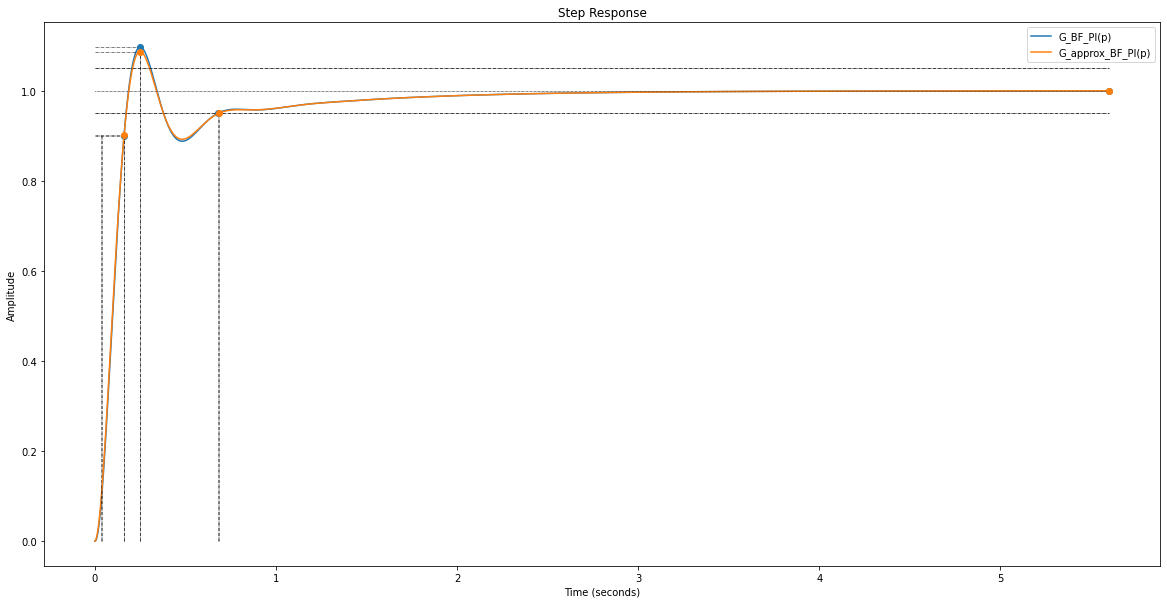
../_images/LaboSeance5_43_1.png ../_images/LaboSeance5_43_2.png

Observations: …

Construction du diagramme de Bode : effet pôle/zéro

Construction de la fonction de transfert d’un correcteur PI de la page 7-8 :

\[ C_{PI}(p)=K_p*\frac{1+\tau_I*p}{\tau_I*p} \]

Prenez \(K_p\) = 10 et \(\tau_I\) = 1s

Tracez l’effet:

  • de \(K_p\)

  • du zéro: \(f_1=1+p\tau_I\)

    et observez l’influence d’un zéro de la fonction de transfert lorsque \(\omega<<<\frac{1}{\tau_I}\) et \(\omega>>>\frac{1}{\tau_I}\) \(\Rightarrow\) synthèse sur l’effet d’un zéro à la page 4-16 !

  • du pôle: \(f_2=\frac{1}{p\tau_I}\)

    et observez l’influence d’un pôle à l’origine

\(\Rightarrow\) Observez la construction de la fonction \(C_{PI}\) par morceaux

\(\Rightarrow\) Observez qu’en HF, le pôle compense le zéro

Kp = 10
tI = 1
f_Kp = ml.tf(Kp, 1)
f1 = ml.tf([tI, 1], [1])
f2 = ml.tf([1], [tI, 0])

fig = plt.figure("", figsize=(20,10))
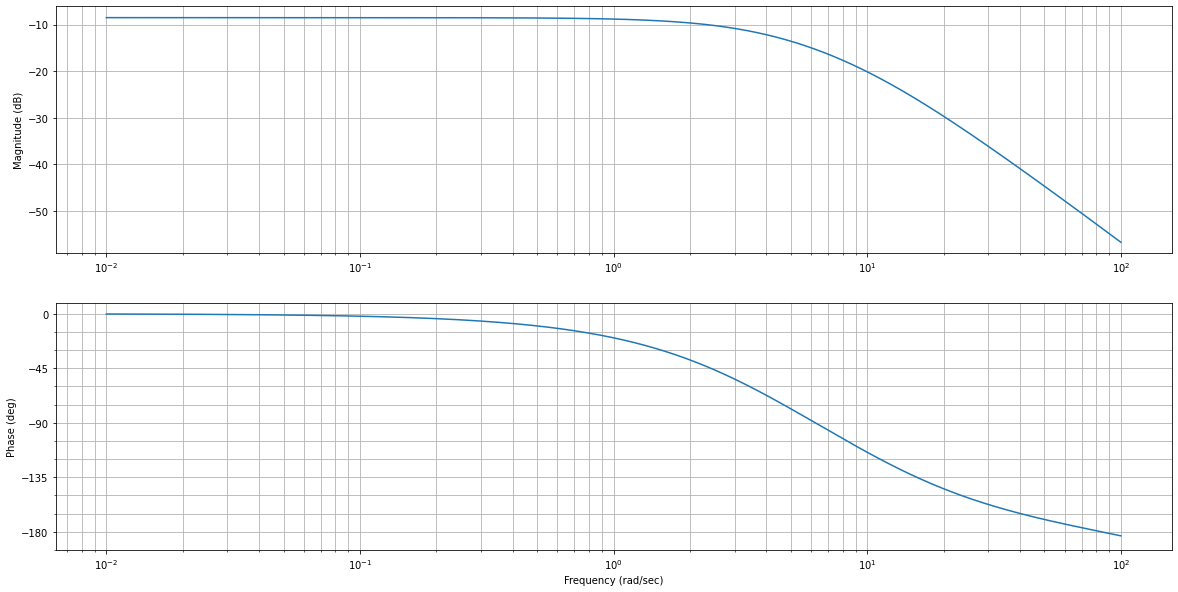
ml.bode(f_Kp)
ml.bode(f1)
ml.bode(f2)
plt.legend(['Kp', 'f1', 'f2']);
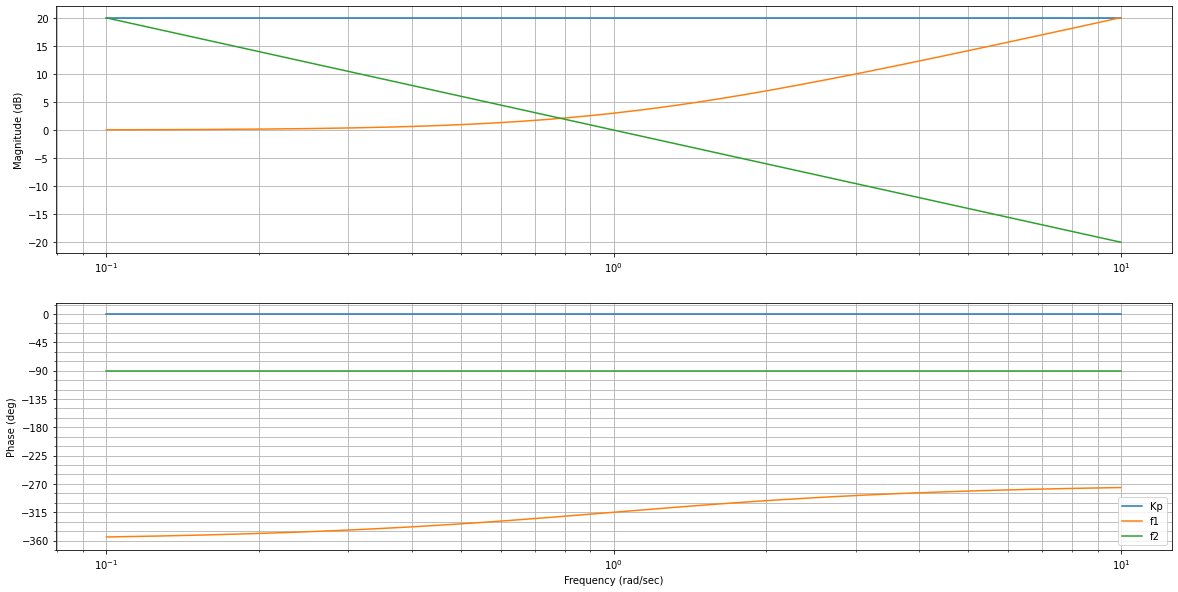
../_images/LaboSeance5_46_0.png

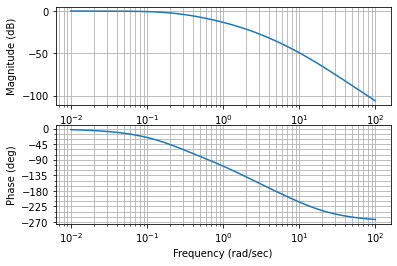
[Facultatif] Construisez le diagramme de Bode de la fonction de transfert de la page 4-17 :

\[ G(p) = K_P*\frac{\tau_1p+1}{(\tau_2p+1)(\tau_3p+1)} \]

Prenez \(\tau_1\)=1s, \(\tau_2\)=10000s, \(\tau_3\) = 0.001s et \(K_P\) = 2

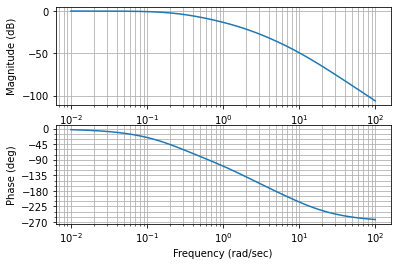
  • Tracez le diagramme de Bode de \(f_2=\frac{1}{\tau_2p+1}\):

tI2 = 10000
f2 = ml.tf([1], [tI2, 1])
fig = plt.figure("", figsize=(20,10))
ml.bode(f2);
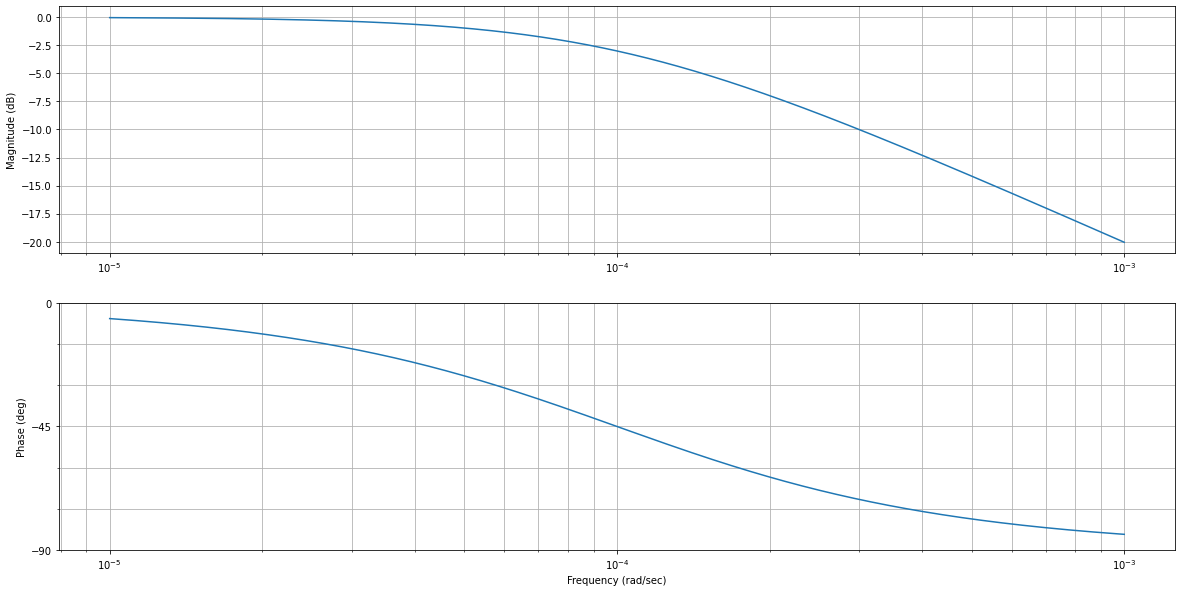
../_images/LaboSeance5_48_0.png

  • Tracez le diagramme de Bode de \(f_1=\tau_1p+1\):

tI1 = 1
f1 = ml.tf([tI1, 1], [1])
fig = plt.figure("", figsize=(20,10))
ml.bode(f1);
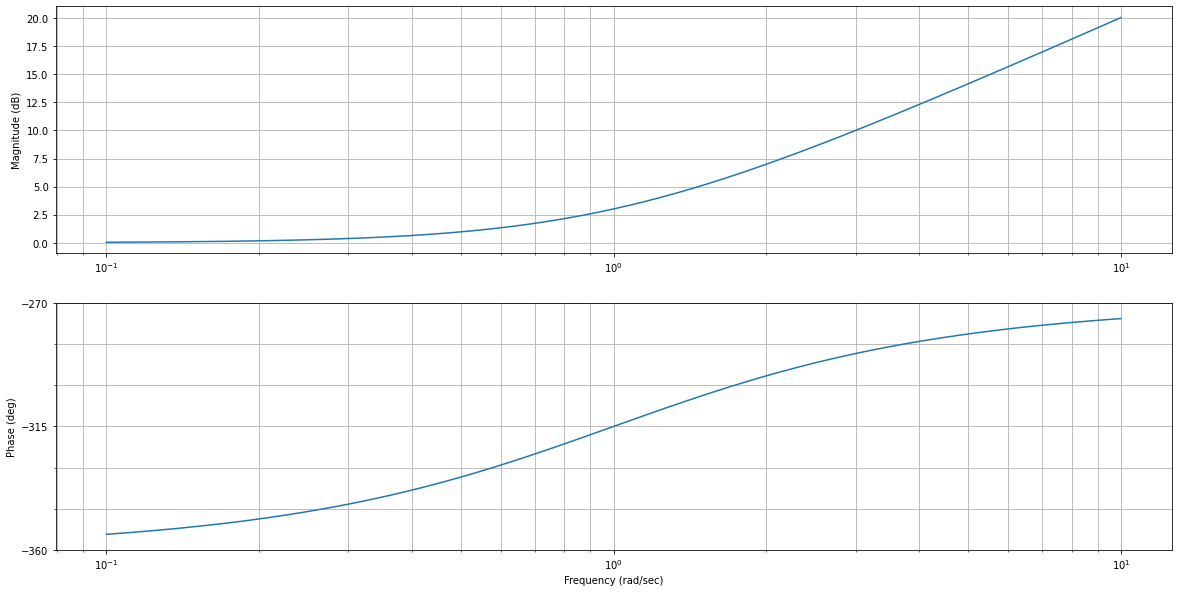
../_images/LaboSeance5_50_0.png

  • Tracez le diagramme de Bode de la fonction finale \(H=f_1*f_2*f_3\) et observez l’addition graphique des différentes contributions :

Kp = 2
tI3 = 0.001
f3 = ml.tf([1], [tI3, 1])

H = Kp*f1*f2*f3
fig = plt.figure("", figsize=(20,10))
ml.bode(H);
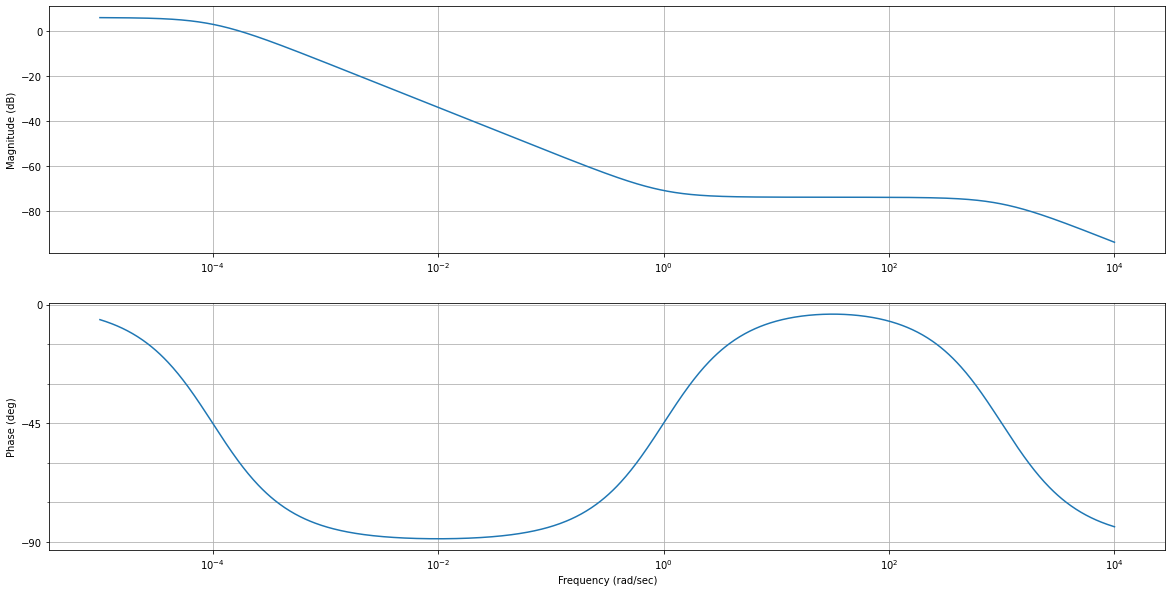
../_images/LaboSeance5_52_0.png

Effet si les pulsations caractéristiques sont plus proches : \(\tau_1=1s\), \(\tau_2=10s\) et \(\tau_3=0,01s\):

tI1 = 1
tI2 = 10
tI3 = 0.01

f1 = ml.tf([tI1, 1], [1])
f2 = ml.tf([1], [tI2, 1])
f3 = ml.tf([1], [tI3, 1])

H = Kp*f1*f2*f3
fig = plt.figure("", figsize=(20,10))
ml.bode(H);
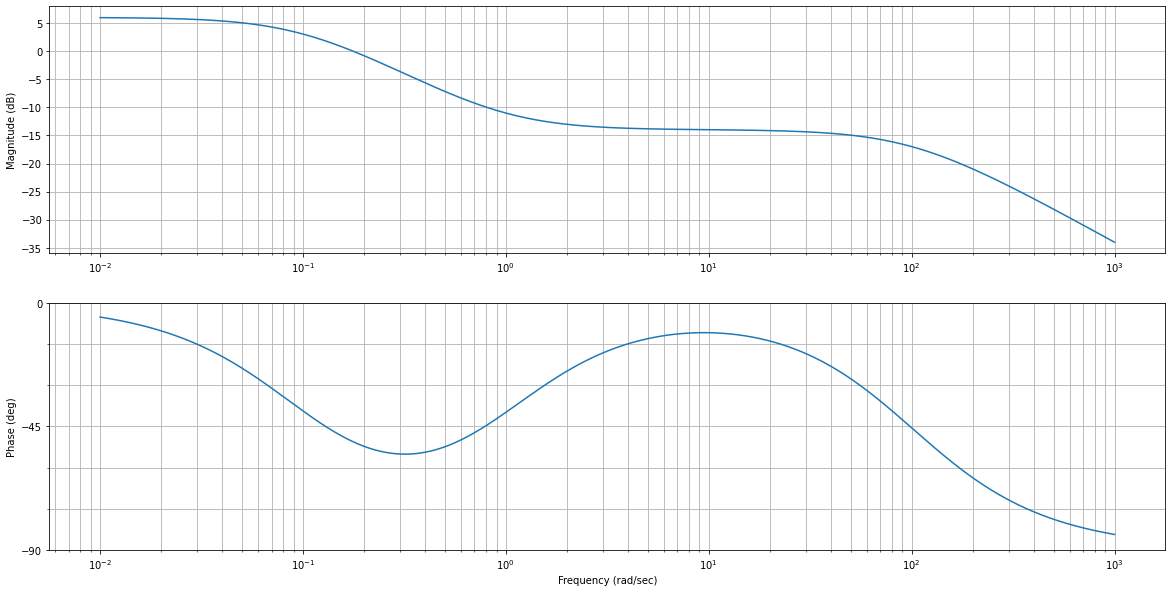
../_images/LaboSeance5_54_0.png

Effet si les pulsations caractéristiques sont dispersées : \(\tau_1=0.001s\), \(\tau_2=10000s\) et \(\tau_3=1s\) et \(K_P=2\):

tI1 = 0.001
tI2 = 10000
tI3 = 1
Kp = 2

f1 = ml.tf([tI1, 1], [1])
f2 = ml.tf([1], [tI2, 1])
f3 = ml.tf([1], [tI3, 1])

H = Kp*f1*f2*f3
fig = plt.figure("", figsize=(20,10))
ml.bode(H);
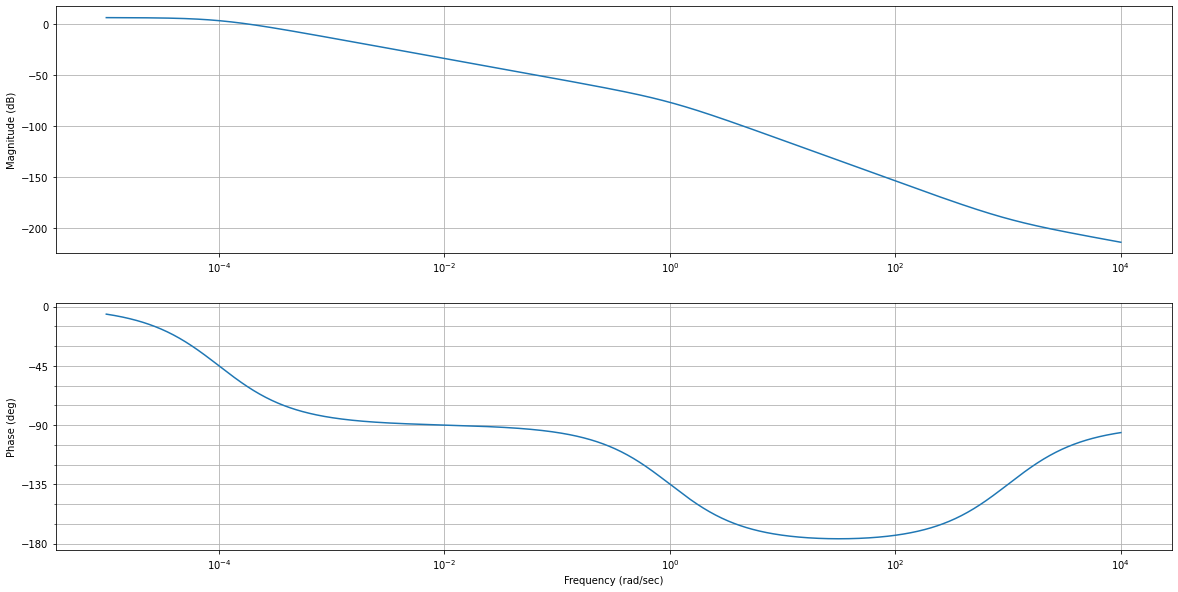
../_images/LaboSeance5_56_0.png

[Facultatif] Exercice 4 page 7-9 (fait au cours)

Soit la fonction de boucle ouverte d’un processus d’asservissement de position:

\[G(p)=\frac {1}{(1+0,1p)(1+0,01p)}\]

Auquel on applique un correcteur PI:

\[C_{PI}=\frac{15.55p+18.42}{0.8445p}\]

Observez l’effet du pôle à l’origine :

  • sur le module :

  • sur la phase :

Comment cela se traduit-il sur la réponse indicielle? :

previous

Séance 4

next

Séance 6